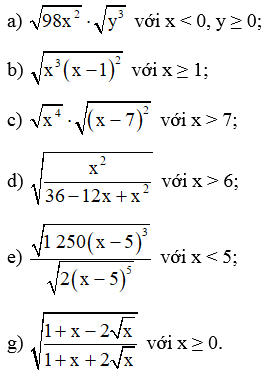Áp dụng quy tắc về căn thức bậc hai của một tích và một thương

Áp dụng quy tắc về căn thức bậc hai của một tích và một thương, hãy rút gọn biểu thức:

Giải SBT Toán 9 Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số - Cánh diều

Bài 32 trang 66 SBT Toán 9 Tập 1: Áp dụng quy tắc về căn thức bậc hai của một tích và một thương, hãy rút gọn biểu thức:

Lời giải:

a) $\sqrt{98x^2}\cdot \sqrt{y^3}=\sqrt{49\cdot 2\cdot x^2}\cdot \sqrt{y^2\cdot y}$

$=7\cdot \left|x\right|\cdot \sqrt{2}\cdot \left|y\right|\cdot \sqrt{y}$

$=-7xy\sqrt{2y}$ (do x < 0, y ≥ 0).

b) $\sqrt{x^3{\left(x-1\right)}^2}=\sqrt{x^2\cdot x\cdot {\left(x-1\right)}^2}=\left|x\right|\cdot \left|x-1\right|\cdot \sqrt{x}.$

Do x ≥ 1 nên x ‒ 1 ≥ 0, do đó |x – 1| = x – 1.

Vậy $\sqrt{x^3{\left(x-1\right)}^2}=\left|x\right|\cdot \left|x-1\right|\cdot \sqrt{x}=x\left(x-1\right)\sqrt{x}.$

c) $\sqrt{x^4}\cdot \sqrt{{\left(x-7\right)}^2}=\sqrt{{\left(x^2\right)}^2}\cdot \left|x-7\right|=\left|x^2\right|\cdot \left|x-7\right|=x^2\cdot \left|x-7\right|$  (do x² > 0 với mọi x > 7).

Do x > 7 nên x ‒ 7 > 0, do đó |x – 7| = x – 7.

Vậy $\sqrt{x^4}\cdot \sqrt{{\left(x-7\right)}^2}=x^2\cdot \left|x-7\right|=x^2\left(x-7\right).$

d) $\sqrt{\frac{x^2}{36-12x+x^2}}=\sqrt{\frac{x^2}{{\left(x-6\right)}^2}}=\sqrt{{\left(\frac{x}{x-6}\right)}^2}=\left|\frac{x}{x-6}\right|.$

Do x > 6 > 0 nên x ‒ 6 > 0, do đó $\frac{x}{x-6}>0,$ suy ra $\left|\frac{x}{x-6}\right|=\frac{x}{x-6}.$

Vậy $\sqrt{\frac{x^2}{36-12x+x^2}}=\left|\frac{x}{x-6}\right|=\frac{x}{x-6}.$

e) $\frac{\sqrt{1250{\left(x-5\right)}^3}}{\sqrt{2{\left(x-5\right)}^5}}=\sqrt{\frac{1250{\left(x-5\right)}^3}{2{\left(x-5\right)}^5}}$

$=\sqrt{\frac{625}{{\left(x-5\right)}^2}}=\sqrt{\frac{{25}^2}{{\left(x-5\right)}^2}}=\sqrt{{\left(\frac{25}{x-5}\right)}^2}=\left|\frac{25}{x-5}\right|.$

Do x < 5 nên x ‒ 5 < 0, do đó $\frac{25}{x-5}<0,$ suy ra $\left|\frac{25}{x-5}\right|=-\frac{25}{x-5}=\frac{25}{5-x}.$

Vậy $\frac{\sqrt{1250{\left(x-5\right)}^3}}{\sqrt{2{\left(x-5\right)}^5}}=\left|\frac{25}{x-5}\right|=\frac{25}{5-x}.$

g) $\sqrt{\frac{1+x-2\sqrt{x}}{1+x+2\sqrt{x}}}=\sqrt{\frac{{\left(\sqrt{x}-1\right)}^2}{{\left(\sqrt{x}+1\right)}^2}}=\sqrt{{\left(\frac{\sqrt{x}-1}{\sqrt{x}+1}\right)}^2}$

$=\left|\frac{\sqrt{x}-1}{\sqrt{x}+1}\right|=\frac{\left|\sqrt{x}-1\right|}{\sqrt{x}+1}$ (do $\sqrt{x}+1>0$ với mọi số thực x ≥ 0).

Lời giải SBT Toán 9 Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số hay khác:

• Bài 31 trang 65 SBT Toán 9 Tập 1: Áp dụng quy tắc về căn thức bậc hai của một bình phương, hãy rút gọn biểu thức: a) $\sqrt{25-10x+x^2}$ với x ≤ 5;....

• Bài 33 trang 66 SBT Toán 9 Tập 1: Trục căn thức ở mẫu: a) $\frac{2-\sqrt{5}}{\sqrt{5}};$....

• Bài 34 trang 66 SBT Toán 9 Tập 1: Trục căn thức ở mẫu: a) $\frac{2}{\sqrt{3x-1}}$ với $x>\frac{1}{3};$....

• Bài 35 trang 66 SBT Toán 9 Tập 1: Chứng minh: a) $\frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}+\frac{\sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}-\frac{\sqrt{5}+1}{\sqrt{5}-1}=\frac{13-\sqrt{5}}{2};$....

• Bài 36 trang 66 SBT Toán 9 Tập 1: a) Cho biểu thức: $A=\frac{1}{3-\sqrt{8}}-\frac{1}{\sqrt{8}-\sqrt{7}}+\frac{1}{\sqrt{7}-\sqrt{6}}-\frac{1}{\sqrt{6}-\sqrt{5}}+\frac{1}{\sqrt{5}-2}.$...

• Bài 37 trang 67 SBT Toán 9 Tập 1: a) Cho biểu thức: $C=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\frac{1}{\sqrt{4}}+\cdots +\frac{1}{\sqrt{24}}+\frac{1}{\sqrt{25}}.$....

• Bài 38 trang 67 SBT Toán 9 Tập 1: Cho biểu thức: $M=\frac{1}{2\sqrt{x}-2}-\frac{1}{2\sqrt{x}+2}+\frac{\sqrt{x}}{1-x}$ với x ≥ 0, x ≠ 1.....

• Bài 39 trang 67 SBT Toán 9 Tập 1: Cho biểu thức: $N=\left(\frac{1}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}\right)\cdot \frac{x+\sqrt{x}}{\sqrt{x}}$ với x > 0.....

• Bài 40 trang 67 SBT Toán 9 Tập 1: Cho biểu thức: $P=\frac{2}{\sqrt{x}-1}+\frac{2}{\sqrt{x}+1}-\frac{5-\sqrt{x}}{x-1}$với x ≥ 0, x ≠ 1.....

• Bài 41 trang 67 SBT Toán 9 Tập 1: Tìm x, biết: a) $\frac{1}{2}\sqrt{x}-\frac{3}{2}\sqrt{9x}+24\sqrt{\frac{x}{64}}=-17$ với x ≥ 0;....