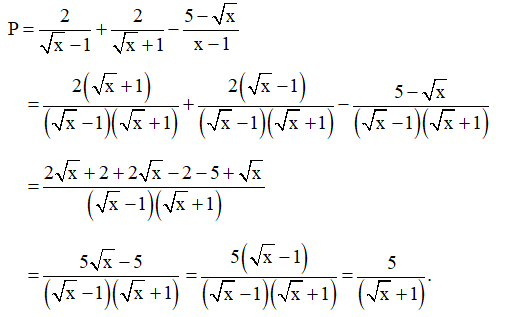Cho biểu thức P, Rút gọn biểu thức P, Tính giá trị của biểu thức P tại x = 4

Cho biểu thức: với x ≥ 0, x ≠ 1.

Giải SBT Toán 9 Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số - Cánh diều

Bài 40 trang 67 SBT Toán 9 Tập 1: Cho biểu thức: $P=\frac{2}{\sqrt{x}-1}+\frac{2}{\sqrt{x}+1}-\frac{5-\sqrt{x}}{x-1}$ với x ≥ 0, x ≠ 1.

a) Rút gọn biểu thức P.

b) Tính giá trị của biểu thức P tại x = 4.

c*) Tìm giá trị của x để P có giá trị là số nguyên.

Lời giải:

a) Với x ≥ 0, x ≠ 1, ta có:

Vậy với x ≥ 0, x ≠ 1 thì $P=\frac{5}{\sqrt{x}+1}.$

b) Thay x = 4 (thỏa mãn điều kiện) vào biểu thức $P=\frac{5}{\sqrt{x}+1},$ ta có:

$P=\frac{5}{\sqrt{4}+1}=\frac{5}{2+1}=\frac{5}{3}.$

Vậy giá trị của biểu thức P tại x = 4 là $\frac{5}{3}$

c*) Với x ≥ 0, x ≠ 1, ta có $\sqrt{x}+1\ge 1$ nên $\frac{5}{\sqrt{x}+1}>0$ và $\frac{5}{\sqrt{x}+1}\le 5.$

Do đó 0 < P ≤ 5.

Vì vậy, để P có giá trị là số nguyên thì P ∈{1; 2; 3; 4; 5}.

⦁ Nếu P = 1 thì $\frac{5}{\sqrt{x}+1}=1,$ suy ra $\sqrt{x}+1=5$ hay $\sqrt{x}=4,$ do đó x = 4² hay x = 16 (thoả mãn x ≥ 0, x ≠ 1).

⦁ Nếu P = 2 thì $\frac{5}{\sqrt{x}+1}=2,$ suy ra $\sqrt{x}+1=\frac{5}{2}$ hay $\sqrt{x}=\frac{3}{2},$ do đó $x={\left(\frac{3}{2}\right)}^2$ hay $x=\frac{9}{4}$ (thoả mãn x ≥ 0, x ≠ 1).

⦁ Nếu P = 3 thì $\frac{5}{\sqrt{x}+1}=3,$ suy ra $\sqrt{x}+1=\frac{5}{3}$ hay $\sqrt{x}=\frac{2}{3},$$x={\left(\frac{2}{3}\right)}^2$ hay $x=\frac{4}{9}$ (thoả mãn x ≥ 0, x ≠ 1).

⦁ Nếu P = 4 thì $\frac{5}{\sqrt{x}+1}=4,$ suy ra $\sqrt{x}+1=\frac{5}{4}$ hay $\sqrt{x}=\frac{1}{4},$ do đó $x={\left(\frac{1}{4}\right)}^2$ hay $x=\frac{1}{16}$ (thoả mãn x ≥ 0, x ≠ 1).

⦁ Nếu P = 5 thì $\frac{5}{\sqrt{x}+1}=5,$ suy ra $\sqrt{x}+1=1$ hay $\sqrt{x}=0,$ do đó x = 0 (thoả mãn x ≥ 0, x ≠ 1).

Vậy $x\in \left\{16;\frac{9}{4};\frac{4}{9};\frac{1}{16};0\right\}$ thì P có giá trị là số nguyên.

Lời giải SBT Toán 9 Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số hay khác:

• Bài 31 trang 65 SBT Toán 9 Tập 1: Áp dụng quy tắc về căn thức bậc hai của một bình phương, hãy rút gọn biểu thức: a) $\sqrt{25-10x+x^2}$ với x ≤ 5;....

• Bài 32 trang 66 SBT Toán 9 Tập 1: Áp dụng quy tắc về căn thức bậc hai của một tích và một thương, hãy rút gọn biểu thức: a) $\sqrt{98x^2}\cdot \sqrt{y^3}$ với x < 0, y ≥ 0;....

• Bài 33 trang 66 SBT Toán 9 Tập 1: Trục căn thức ở mẫu: a) $\frac{2-\sqrt{5}}{\sqrt{5}};$....

• Bài 34 trang 66 SBT Toán 9 Tập 1: Trục căn thức ở mẫu: a) $\frac{2}{\sqrt{3x-1}}$ với $x>\frac{1}{3};$....

• Bài 35 trang 66 SBT Toán 9 Tập 1: Chứng minh: a) $\frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}+\frac{\sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}-\frac{\sqrt{5}+1}{\sqrt{5}-1}=\frac{13-\sqrt{5}}{2};$....

• Bài 36 trang 66 SBT Toán 9 Tập 1: a) Cho biểu thức: $A=\frac{1}{3-\sqrt{8}}-\frac{1}{\sqrt{8}-\sqrt{7}}+\frac{1}{\sqrt{7}-\sqrt{6}}-\frac{1}{\sqrt{6}-\sqrt{5}}+\frac{1}{\sqrt{5}-2}.$...

• Bài 37 trang 67 SBT Toán 9 Tập 1: a) Cho biểu thức: $C=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\frac{1}{\sqrt{4}}+\cdots +\frac{1}{\sqrt{24}}+\frac{1}{\sqrt{25}}.$....

• Bài 38 trang 67 SBT Toán 9 Tập 1: Cho biểu thức: $M=\frac{1}{2\sqrt{x}-2}-\frac{1}{2\sqrt{x}+2}+\frac{\sqrt{x}}{1-x}$ với x ≥ 0, x ≠ 1.....

• Bài 39 trang 67 SBT Toán 9 Tập 1: Cho biểu thức: $N=\left(\frac{1}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}\right)\cdot \frac{x+\sqrt{x}}{\sqrt{x}}$ với x > 0.....

• Bài 41 trang 67 SBT Toán 9 Tập 1: Tìm x, biết: a) $\frac{1}{2}\sqrt{x}-\frac{3}{2}\sqrt{9x}+24\sqrt{\frac{x}{64}}=-17$ với x ≥ 0;....