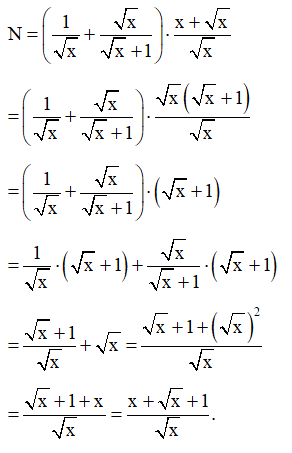Cho biểu thức N = (1/√x + √x/(√x +1). (x+√x) với x > 0

Cho biểu thức: với x > 0.

Giải SBT Toán 9 Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số - Cánh diều

Bài 39 trang 67 SBT Toán 9 Tập 1: Cho biểu thức: $N=\left(\frac{1}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}\right)\cdot \frac{x+\sqrt{x}}{\sqrt{x}}$ với x > 0.

a) Rút gọn biểu thức N.

b*) Tìm giá trị nhỏ nhất của N.

Lời giải:

a) Với x > 0, ta có:

Vậy với x > 0 thì $N=\frac{x+\sqrt{x}+1}{\sqrt{x}}.$

b*) Với x > 0, ta có: $N=\frac{x+\sqrt{x}+1}{\sqrt{x}}=\sqrt{x}+1+\frac{1}{\sqrt{x}}$.

Do $\sqrt{x}>0$ và $\frac{1}{\sqrt{x}}>0$ với x > 0 nên theo kết quả Ví dụ 5 (trang 65), SBT Toán 9, Tập một, ta có: $\sqrt{x}+\frac{1}{\sqrt{x}}\ge 2\sqrt{\sqrt{x}\cdot \frac{1}{\sqrt{x}}}$ hay $\sqrt{x}+\frac{1}{\sqrt{x}}\ge 2,$ suy ra $\sqrt{x}+\frac{1}{\sqrt{x}}+1\ge 2+1$ hay N ≥ 3.

Vậy giá trị nhỏ nhất của N là 3 khi $\sqrt{x}=\frac{1}{\sqrt{x}}$ hay x = 1 (thoả mãn x > 0).

Lời giải SBT Toán 9 Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số hay khác:

• Bài 31 trang 65 SBT Toán 9 Tập 1: Áp dụng quy tắc về căn thức bậc hai của một bình phương, hãy rút gọn biểu thức: a) $\sqrt{25-10x+x^2}$ với x ≤ 5;....

• Bài 32 trang 66 SBT Toán 9 Tập 1: Áp dụng quy tắc về căn thức bậc hai của một tích và một thương, hãy rút gọn biểu thức: a) $\sqrt{98x^2}\cdot \sqrt{y^3}$ với x < 0, y ≥ 0;....

• Bài 33 trang 66 SBT Toán 9 Tập 1: Trục căn thức ở mẫu: a) $\frac{2-\sqrt{5}}{\sqrt{5}};$....

• Bài 34 trang 66 SBT Toán 9 Tập 1: Trục căn thức ở mẫu: a) $\frac{2}{\sqrt{3x-1}}$ với $x>\frac{1}{3};$....

• Bài 35 trang 66 SBT Toán 9 Tập 1: Chứng minh: a) $\frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}+\frac{\sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}-\frac{\sqrt{5}+1}{\sqrt{5}-1}=\frac{13-\sqrt{5}}{2};$....

• Bài 36 trang 66 SBT Toán 9 Tập 1: a) Cho biểu thức: $A=\frac{1}{3-\sqrt{8}}-\frac{1}{\sqrt{8}-\sqrt{7}}+\frac{1}{\sqrt{7}-\sqrt{6}}-\frac{1}{\sqrt{6}-\sqrt{5}}+\frac{1}{\sqrt{5}-2}.$...

• Bài 37 trang 67 SBT Toán 9 Tập 1: a) Cho biểu thức: $C=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\frac{1}{\sqrt{4}}+\cdots +\frac{1}{\sqrt{24}}+\frac{1}{\sqrt{25}}.$....

• Bài 38 trang 67 SBT Toán 9 Tập 1: Cho biểu thức: $M=\frac{1}{2\sqrt{x}-2}-\frac{1}{2\sqrt{x}+2}+\frac{\sqrt{x}}{1-x}$ với x ≥ 0, x ≠ 1.....

• Bài 40 trang 67 SBT Toán 9 Tập 1: Cho biểu thức: $P=\frac{2}{\sqrt{x}-1}+\frac{2}{\sqrt{x}+1}-\frac{5-\sqrt{x}}{x-1}$với x ≥ 0, x ≠ 1.....

• Bài 41 trang 67 SBT Toán 9 Tập 1: Tìm x, biết: a) $\frac{1}{2}\sqrt{x}-\frac{3}{2}\sqrt{9x}+24\sqrt{\frac{x}{64}}=-17$ với x ≥ 0;....