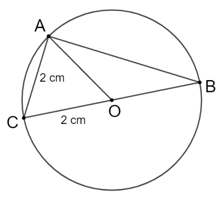
Cho tam giác ABC vuông tại A nội tiếp đường tròn (O) có bán kính 2 cm. Biết rằng AC = 2 cm, tính số đo các góc của tam giác ABC

Cho tam giác ABC vuông tại A nội tiếp đường tròn (O) có bán kính 2 cm. Biết rằng AC = 2 cm, tính số đo các góc của tam giác ABC.

Giải sách bài tập Toán 9 Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác - Kết nối tri thức

Bài 9.14 trang 53 sách bài tập Toán 9 Tập 2: Cho tam giác ABC vuông tại A nội tiếp đường tròn (O) có bán kính 2 cm. Biết rằng AC = 2 cm, tính số đo các góc của tam giác ABC.

Lời giải:

Do tam giác ABC vuông tại A nên tâm O của đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh BC.

Do đó tam giác AOC có: OA = OC = AC = 2 cm.

Suy ra tam giác AOC là tam giác đều.

Từ đó ta có $\widehat{ACO}=\widehat{AOC}$.

Vì vậy $\widehat{ACB}=\widehat{ACO}$ = 60°.     

Mặt khác, góc nội tiếp ABC và góc ở tâm AOC của (O) cùng chắn cung nhỏ $\stackrel{⏜}{AC}$ nên $\widehat{ABC}=\frac{1}{2}\widehat{AOC}=\frac{60°}{2}=30°$

Tam giác ABC vuông tại A nên $\widehat{BAC}=90°$

Vậy $\widehat{ACB}=60°, \widehat{ABC}=30°, \widehat{BAC}=90°$

Lời giải SBT Toán 9 Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác hay khác:

• Bài 9.8 trang 53 sách bài tập Toán 9 Tập 2: Cho tam giác ABC nội tiếp đường tròn (O). Biết rằng $\widehat{ACB}=50°,\widehat{ABC}=70°,$ tính số đo các cung nhỏ $\stackrel{⏜}{BC},\stackrel{⏜}{CA},\stackrel{⏜}{AB}$ của đường tròn (O). ...

• Bài 9.9 trang 53 sách bài tập Toán 9 Tập 2: Cho tam giác ABC cân tại A và nội tiếp đường tròn (O). Tính số đo các góc của tam giác ABC, biết rằng $\widehat{BOC}=100°.$ ...

• Bài 9.10 trang 53 sách bài tập Toán 9 Tập 2: Tính bán kính và chu vi của đường tròn ngoại tiếp tam giác ABC có ba cạnh AB = 6 cm, AC = 8 cm và BC =10 cm ...

• Bài 9.11 trang 53 sách bài tập Toán 9 Tập 2: Tính chu vi và diện tích của tam giác đều nội tiếp một đường tròn bán kính 3 cm ...

• Bài 9.12 trang 53 sách bài tập Toán 9 Tập 2: Tính chu vi và diện tích của tam giác đều ngoại tiếp một đường tròn bán kính 3 cm ...

• Bài 9.13 trang 53 sách bài tập Toán 9 Tập 2: Cho tam giác ABC vuông tại Acó AB = 4 cm, AC = 6 cm. Tính bán kính của đường tròn nội tiếp tam giác ABC ...

• Bài 9.15 trang 53 sách bài tập Toán 9 Tập 2: Cho tam giác ABC có trực tâm H và nội tiếp đường tròn (O). Chứng minh rằng ...

• Bài 9.16 trang 53 sách bài tập Toán 9 Tập 2: Cho tam giác ABC ngoại tiếp đường tròn (I). Chứng minh rằng: ...

• Bài 9.17 trang 53 sách bài tập Toán 9 Tập 2: Cho tam giác nhọn ABC nội tiếp đường tròn (O). Cho điểm M trên cạnh BC của tam giác ABC và điểm D ...

• Bài 9.18 trang 54 sách bài tập Toán 9 Tập 2: Cho tam giác ABC vuông tại B nội tiếp đường tròn (O) và đường kính BD. Tính số đo của góc BAC, biết rằng $\widehat{BAC}=2\widehat{CBD}$ ...

• Bài 9.19 trang 54 sách bài tập Toán 9 Tập 2: Cho tam giác ABC nội tiếp đường tròn (O) và ngoại tiếp đường tròn (I). Tia AI cắt (O) tại X (khác A) ...

• Bài 9.20 trang 54 sách bài tập Toán 9 Tập 2: Cho ∆ABC ᔕ ∆A'B'C' với tỉ số đồng dạng k > 0. Gọi (O; R) và (O'; R') lần lượt là đường tròn ngoại tiếp các tam giác ABC và A'B'C ...