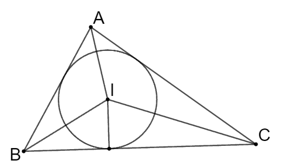
Cho tam giác ABC ngoại tiếp đường tròn (I). Chứng minh rằng

Cho tam giác ABC ngoại tiếp đường tròn (I). Chứng minh rằng:

Giải sách bài tập Toán 9 Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác - Kết nối tri thức

Bài 9.16 trang 53 sách bài tập Toán 9 Tập 2: Cho tam giác ABC ngoại tiếp đường tròn (I). Chứng minh rằng:

$\hat{B I C} = 90 ° + \frac{\hat{B A C}}{2}; \hat{C I A} = 90 ° + \frac{\hat{C B A}}{2}; \hat{A I B} = 90 ° + \frac{\hat{A C B}}{2}$

Lời giải:

Cho tam giác ABC ngoại tiếp đường tròn (I). Chứng minh rằng

Vì I là giao điểm các đường phân giác của tam giác ABC nên ta có:

$\hat{I B C} = \frac{\hat{A B C}}{2}; \hat{I C B} = \frac{\hat{A C B}}{2}$ .

Vì tổng các góc trong tam giác ABC bằng 180° nên ta có:

$\hat{I B C} + \hat{I C B} = \frac{\hat{A B C} + \hat{A C B}}{2} = \frac{180 ° - \hat{B A C}}{2} = 90 ° - \frac{\hat{B A C}}{2}$

Vì tổng các góc trong tam giác BIC bằng 180° nên ta có:

$\hat{B I C} = 180 ° - \hat{I B C} - \hat{I C B} = 180 ° - (90 ° - \frac{\hat{B A C}}{2}) = 90 ° + \frac{\hat{B A C}}{2}$ . (đpcm)

Tương tự, ta có $\hat{C I A} = 90 ° + \frac{\hat{C B A}}{2}; \hat{A I B} = 90 ° + \frac{\hat{A C B}}{2}$ (đpcm).

Lời giải SBT Toán 9 Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác hay khác: