Cho ∆ABC ᔕ ∆A'B'C' với tỉ số đồng dạng k > 0. Gọi (O; R) và (O'; R') lần lượt là đường tròn ngoại tiếp

❮ Bài trước Bài sau ❯

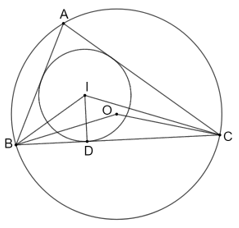
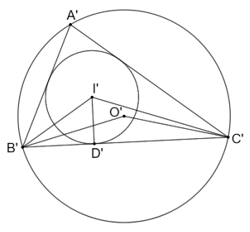
Cho ∆ABC ᔕ ∆A'B'C' với tỉ số đồng dạng k > 0. Gọi (O; R) và (O'; R') lần lượt là đường tròn ngoại tiếp các tam giác ABC và A'B'C'. Gọi (I; r) và (I'; r') lần lượt là đường tròn nội tiếp các tam giác ABC và A'B'C'. Chứng minh rằng

Giải sách bài tập Toán 9 Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác - Kết nối tri thức

Bài 9.20 trang 54 sách bài tập Toán 9 Tập 2: Cho ∆ABC ᔕ ∆A'B'C' với tỉ số đồng dạng k > 0. Gọi (O; R) và (O'; R') lần lượt là đường tròn ngoại tiếp các tam giác ABC và A'B'C'. Gọi (I; r) và (I'; r') lần lượt là đường tròn nội tiếp các tam giác ABC và A'B'C'. Chứng minh rằng $\frac{R}{R'} = \frac{r}{r'} = k$

Lời giải:

Cho ∆ABC ᔕ ∆A'B'C' với tỉ số đồng dạng k > 0. Gọi (O; R) và (O'; R') lần lượt là đường tròn ngoại tiếp

Các góc BOC và BAC là góc ở tâm và góc nội tiếp của (O) cùng chắn cung $\overset{⏜}{B C}$ nên $\hat{B O C} = 2 \hat{B A C}$

Các góc B'O'C' và B'A'C' là góc ở tâm và góc nội tiếp của (O') cùng chắn cung $\overset{⏜}{B' C'}$ nên $\hat{B' O' C'} = 2 \hat{B' A' C'}$

Xét tam giác BOC và tam giác B'O'C' ta có:

$\hat{B O C} = 2 \hat{B A C} = 2 \hat{B' A' C'} = \hat{B' O' C'};$

$\hat{C B O} = \frac{180 ° - \hat{B O C}}{2} = \frac{180 ° - \hat{B' O' C'}}{2} = \hat{C' B' O'}$

Do đó ∆BOC ᔕ ∆B'O'C' (g.g).

Suy ra $\frac{R}{R'} = \frac{O B}{O' B'} = \frac{B C}{B' C'} = k$

Xét tam giác BIC và tam giác B'I'C' ta có:

$\hat{I B C} = \frac{\hat{A B C}}{2} = \frac{\hat{A' B' C'}}{2} = \hat{I' B' C'};$

$\hat{I C B} = \frac{\hat{A C B}}{2} = \frac{\hat{A' C' B'}}{2} = \hat{I' C' B'}$

Do đó ∆BIC ᔕ ∆B'I'C' (g.g).

Suy ra $\frac{I B}{I' B'} = \frac{B C}{B' C'} = k$

Gọi D và D' lần lượt là chân đường vuông góc hạ từ I, I' xuống BC, B'C', ta có:

$\frac{r}{r'} = \frac{I D}{I' D'} = \frac{I B \cos \hat{I B C}}{I' B' \cos \hat{I' B' C'}} = \frac{I B}{I' B'} = k$

Vậy $\frac{R}{R'} = \frac{r}{r'} = k$ (đpcm).

Lời giải SBT Toán 9 Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác hay khác:

SBT Toán 9 Kết nối tri thức

Cho ∆ABC ᔕ ∆A'B'C' với tỉ số đồng dạng k > 0. Gọi (O; R) và (O'; R') lần lượt là đường tròn ngoại tiếp

Giải sách bài tập Toán 9 Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác - Kết nối tri thức

Xem thêm giải sách bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác: