Bài 2 trang 54 Toán 10 Tập 1 Cánh diều
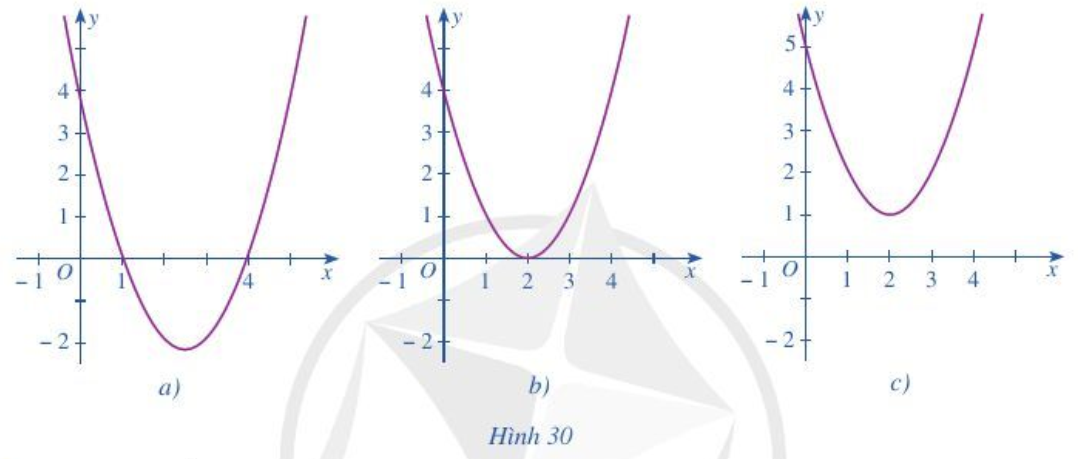
Dựa vào đồ thị hàm số bậc hai y = f(x) trong mỗi Hình 30a, 30b, 30c, hãy viết tập nghiệm của mỗi bất phương trình sau: f(x) > 0, f(x) < 0; f(x) ≥ 0; f(x) ≤ 0.
Giải Toán lớp 10 Bài 4: Bất phương trình bậc hai một ẩn
Bài 2 trang 54 Toán lớp 10 Tập 1: Dựa vào đồ thị hàm số bậc hai y = f(x) trong mỗi Hình 30a, 30b, 30c, hãy viết tập nghiệm của mỗi bất phương trình sau: f(x) > 0, f(x) < 0; f(x) ≥ 0; f(x) ≤ 0.
Lời giải:
a) Quan sát đồ thị Hình 30 a, ta thấy:
+ f(x) > 0 biểu diễn phần parabol y = f(x) nằm phía trên trục hoành, tương ứng với x < 1 hoặc x > 4.
Do đó tập nghiệm của bất phương trình f(x) > 0 là (– ∞; 1) ∪ (4; + ∞).
Và tập nghiệm của bất phương trình f(x) ≥ 0 là (– ∞; 1] ∪ [4; + ∞).
+ f(x) < 0 biểu diễn phần parabol y = f(x) nằm phía dưới trục hoành, tương ứng với 1 < x < 4.
Do đó tập nghiệm của bất phương trình f(x) < 0 là (1; 4).
Và tập nghiệm của bất phương trình f(x) ≤ 0 là [1; 4].
b) Quan sát đồ thị Hình 30 b, ta thấy:
Tại x = 2 thì f(x) = 0.
+ f(x) > 0 biểu diễn phần parabol y = f(x) nằm phía trên trục hoành, tương ứng với x ≠ 2.
Do đó tập nghiệm của bất phương trình f(x) > 0 là .
Và tập nghiệm của bất phương trình f(x) ≥ 0 là .
+ f(x) < 0 biểu diễn phần parabol y = f(x) nằm phía dưới trục hoành, mà phần đồ thị nằm phía trên trục hoành.
Do đó bất phương trình f(x) < 0 vô nghiệm.
Và nghiệm của bất phương trình f(x) ≤ 0 là x = 2.
c) Quan sát đồ thị Hình 30 c, ta thấy phần parabol nằm hoàn toàn phía trên trục hoành, do đó f(x) > 0 với mọi .
Vậy tập nghiệm của bất phương trình f(x) > 0 là và các bất phương trình f(x) < 0, f(x) ≥ 0, f(x) ≤ 0 vô nghiệm.
Lời giải bài tập Toán 10 Bài 4: Bất phương trình bậc hai một ẩn hay, chi tiết khác:
Luyện tập 1 trang 49 Toán lớp 10 Tập 1: Cho hai ví dụ về bất phương trình bậc hai một ẩn. ....
Luyện tập 2 trang 50 Toán lớp 10 Tập 1: Giải các bất phương trình bậc hai sau: ....
Hoạt động 3 trang 50, 51 Toán lớp 10 Tập 1: Cho bất phương trình x2 – 4x + 3 > 0 (2). ....