Cho tam giác ABC đều cạnh a. Tính | vecto AB+ vecto AC|
Câu hỏi:
Cho tam giác ABC đều cạnh a. Tính
A.
B.
C.
D.
Trả lời:
Đáp án đúng là: A
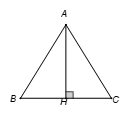
Gọi H là trung điểm của
Xét tam giác vuông AHC ta có:
Suy ra
Ta lại có
Suy ra :
Câu hỏi:
Cho tam giác ABC đều cạnh a. Tính
A.
B.
C.
D.
Trả lời:
Đáp án đúng là: A

Gọi H là trung điểm của
Xét tam giác vuông AHC ta có:
Suy ra
Ta lại có
Suy ra :
Câu 3:
Cho tam giác ABC, có bao nhiêu vectơ khác vectơ - không, có điểm đầu và điểm cuối là các đỉnh A, B, C.
Câu 4:
Cho lục giác đều ABCDEF tâm O. Số các vectơ khác vectơ - không, cùng phương với có điểm đầu và điểm cuối là các đỉnh của lục giác là
Câu 6:
Cho góc . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng:
Câu 7:
Cho tam giác ABC, gọi M là trung điểm AB và N là một điểm trên cạnh AC sao cho . Gọi K là trung điểm của MN. Khi đó :
Câu 8:
Cho hai vectơ và thỏa mãn và hai vectơ và vuông góc với nhau. Xác định góc giữa hai vectơ và .
