Cho tam giác ABC đều cạnh a. Tính | vecto AB+ vecto AC|
Câu hỏi:
Cho tam giác ABC đều cạnh a. Tính |→AB+→AC|.
A. |→AB+→AC|=a√3;
B. |→AB+→AC|=a√32;
C. |→AB+→AC|=2a
D. |→AB+→AC|=2a√3
Trả lời:
Đáp án đúng là: A
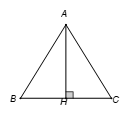
Gọi H là trung điểm của BC⇒AH⊥BC.
Xét tam giác vuông AHC ta có:
AH2+HC2=AC2
⇔AH=√AC2−HC2
⇔AH=√a2−a24
Suy ra AH=BC√32=a√32.
Ta lại có |→AB+→AC|=|→AH+→HB+→AH+→HC|=|2→AH|
Suy ra : |2→AH|=2.a√32=a√3
Xem thêm bài tập Toán 10 Cánh diều có lời giải hay khác:
Câu 1:
Cho ba điểm A, B, C phân biệt. Khẳng định nào sau đây đúng?
Xem lời giải »
Câu 2:
Cho →a và →b là các vectơ khác →0 với →a là vectơ đối của →b. Khẳng định nào sau đây sai?
Xem lời giải »
Câu 3:
Cho ba điểm phân biệt A, B, C. Đẳng thức nào sau đây đúng?
Xem lời giải »
Câu 5:
Cho tam giác ABC vuông cân tại A có AB = a. Tính |→AB+→AC|
Xem lời giải »
Câu 6:
Cho tam giác ABC vuông cân tại C và AB=√2. Tính độ dài của →AB+→AC.
Xem lời giải »
Câu 7:
Cho tam giác ABC vuông tại A và có AB=3, AC=4. Tính |→CA+→AB|.
Xem lời giải »
Câu 8:
Cho 5 điểm bất kỳ A, B, C, D, E. Tính tổng →CD+→EC+→DA+→BE
Xem lời giải »
