Giải Toán 10 trang 36 Tập 1 Cánh diều
Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 36 Tập 1 trong Bài 1: Hàm số và đồ thị Toán lớp 10 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 36.
Giải Toán 10 trang 36 Tập 1 Cánh diều
Hoạt động 5 trang 36 Toán lớp 10 Tập 1: Cho hàm số f(x) = x + 1.
a) So sánh f(1) và f(2).
b) Chứng minh rằng nếu sao cho x1 < x2 thì f(x1) < f(x2).
Lời giải:
a) Ta có: f(x) = x + 1.
Khi đó: f(1) = 1 + 1 = 2, f(2) = 2 + 1 = 3
Vì 2 < 3 nên f(1) < f(2).
Vậy f(1) < f(2).
b) Ta có: f(x1) = x1 + 1, f(x2) = x2 + 1
Vì x1 < x2 nên x1 + 1 < x2 + 1 (liên hệ giữa thứ tự và phép cộng)
Do đó: f(x1) < f(x2) với mọi .
Luyện tập 6 trang 36 Toán lớp 10 Tập 1: Chứng tỏ rằng hàm số y = 6x2 nghịch biến trên khoảng (– ∞; 0).
Lời giải:
Hàm số y = 6x2 có nghĩa với mọi x ∈ ℝ nên hàm số y = 6x2 có nghĩa với mọi x ∈ (– ∞; 0).
Xét hai số bất kì x1, x2 ∈ (– ∞; 0) sao cho x1 < x2.
Ta có x1 < x2 < 0 nên hay f(x1) > f(x2).
Vậy hàm số nghịch biến trên khoảng (– ∞; 0).
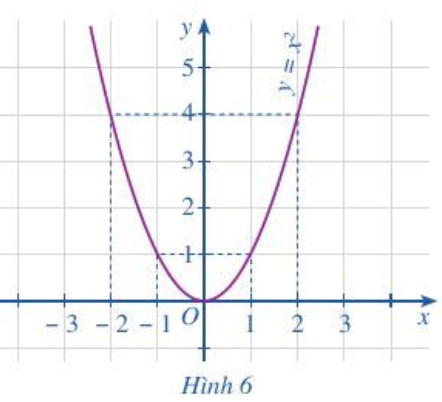
Hoạt động 6 trang 36, 37 Toán lớp 10 Tập 1: Cho đồ thị hàm số: y = f(x) = x2 như Hình 6.
a) So sánh f(– 2), f(– 1). Nêu nhận xét về sự biến thiên của giá trị hàm số khi giá trị biến x tăng dần từ – 2 đến – 1.
b) So sánh f(1), f(2). Nêu nhận xét về sự biến thiên của giá trị hàm số khi giá trị biến x tăng dần từ 1 đến 2.
Lời giải:
a) Quan sát đồ thị hàm số ta thấy: f(– 2) = 4, f(– 1) = 1.
Vì 4 > 1 nên f(– 2) > f(– 1).
Khi giá trị biến x tăng dần từ – 2 đến – 1 thì giá trị của hàm số giảm dần từ 4 xuống 1.
b) Quan sát đồ thị hàm số ta thấy: f(1) = 1, f(2) = 4.
Vì 1 < 4 nên f(1) < f(2).
Khi giá trị biến x tăng dần từ 1 đến 2 thì giá trị của hàm số tăng dần từ 1 lên 4.
Lời giải bài tập Toán lớp 10 Bài 1: Hàm số và đồ thị Cánh diều hay khác: