Giải Toán 10 trang 38 Tập 1 Cánh diều

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 38 Tập 1 trong Bài 1: Hàm số và đồ thị Toán lớp 10 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 38.

Giải Toán 10 trang 38 Tập 1 Cánh diều

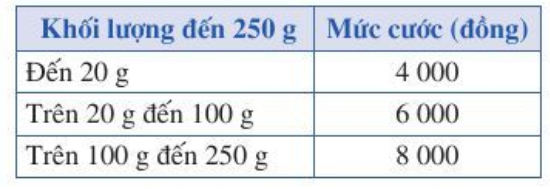
Bài 3 trang 38 Toán lớp 10 Tập 1: Theo quyết định số 2019/QĐ-BĐVN ngày 01/11/2018 của Tổng công ty Bưu điện Việt Nam, giá cước dịch vụ Bưu chính phổ cập đối với dịch vụ thư cơ bản và bưu thiếp trong nước có khối lượng đến 250 g như trong bảng sau:

a) Số tiền dịch vụ thư cơ bản phải trả y (đồng) có là hàm số của khối lượng thư cơ bản x (g) hay không? Nếu đúng, hãy xác định những công thức tính y. 

b) Tính số tiền phải trả khi bạn Dương gửi thư có khối lượng 150g, 200g. 

Lời giải:

 a) Số tiền dịch vụ thư cơ bản phải trả y là hàm số của x vì với mỗi giá trị của x (chính là khối lượng của thư) có đúng một giá trị của y (mức cước hay số tiền phải trả) tương ứng. 

Quan sát bảng ta thấy:

+ Nếu khối lượng thư đến 20 g hay 0 < x ≤ 20 thì mức cước phải trả là 4 000 đồng  hay y = 4 000. 

+ Nếu khối lượng thư trên 20 g đến 100 g hay 20 < x ≤ 100 thì mức cước là 6 000 đồng hay y = 6 000. 

+ Nếu khối lượng thư trên 100 g đến 250 g hay 100 < x ≤ 250 thì mức cước là 8 000 đồng hay y = 8 000. 

Vậy ta có công thức xác định y như sau:  

$y=\left\{\begin{array}{l}4000n{ê}^{\text{'}}u0<x\le 20\\ 6000n{ê}^{\text{'}}u20<x\le 100\\ 8000n{ê}^{\text{'}}u100<x\le 250\end{array}\right.$

b) Vì 100 < 150 < 250 và 100 < 200 < 250 nên bức thư có khối lượng 150 g thì cần trả cước là 8 000 đồng và bức thư có khối lượng 200 g cũng cần trả cước là 8 000 đồng. 

Vậy tổng số tiền phải trả khi bạn Dương gửi thư có khối lượng 150 g, 200 g là: 

8 000 + 8 000 = 16 000 (đồng). 

Bài 4 trang 38 Toán lớp 10 Tập 1: Cho hàm số y = – 2x².

a) Tìm những điểm thuộc đồ thị hàm số có hoành độ lần lượt bằng – 2; 3 và 10.

b) Tìm những điểm thuộc đồ thị hàm số có tung độ bằng – 18. 

Lời giải:

a) Điểm có hoành độ bằng – 2 hay x = – 2 thì tung độ y = (– 2) . (– 2)² = – 8.

Điểm có hoành độ bằng 3 hay x = 3 thì tung độ y = (– 2) . 3² = – 18.

Điểm có hoành độ bằng 10 hay x = 10 thì tung độ y = (– 2) . 10² = – 200. 

Vậy các điểm cần tìm có tọa độ là (– 2; – 8), (3; – 18) và (10; – 200). 

b) Điểm có tung độ bằng – 18 hay y = – 18.

Khi đó: – 2x² = – 18 ⇔ x² = 9 ⇔ x = ± 3. 

Vậy các điểm thuộc đồ thị hàm số có tung độ bằng – 18 là (3; – 18) và (– 3; – 18). 

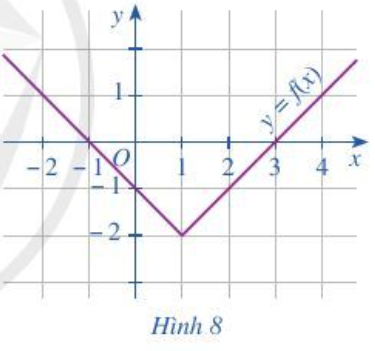
Bài 5 trang 38 Toán lớp 10 Tập 1: Cho đồ thị hàm số y = f(x) như Hình 8.

a) Trong các điểm có tọa độ (1; – 2), (0; 0), (2; – 1), điểm nào thuộc đồ thị hàm số? Điểm nào không thuộc đồ thị hàm số? 

b) Xác định f(0); f(3).

c) Tìm điểm thuộc đồ thị hàm số có tung độ bằng 0. 

Lời giải:

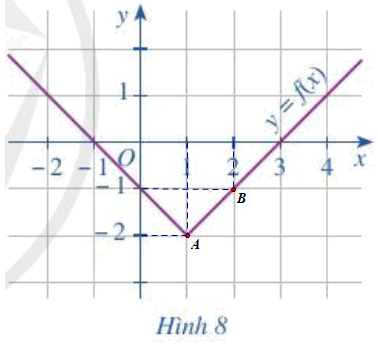
 a) Xác định các điểm A(1; – 2), O(0; 0) và B(2; – 1) lên mặt phẳng tọa độ ở Hình 8:

Quan sát Hình ta thấy:

+ Đồ thị hàm số không đi qua điểm O(0; 0) nên điểm O(0; 0) không thuộc đồ thị hàm số y = f(x). 

+ Đồ thị hàm số đi qua hai điểm A, B nên hai điểm A(1; – 2) và B(2; – 1) thuộc đồ thị hàm số y = f(x). 

b) Ta có f(0) là giá trị của hàm số tại x = 0, mà theo đồ thị ta thấy x = 0 thì y = – 1 (do điểm có tọa độ (0; – 1) thuộc đồ thị hàm số) nên f(0) = – 1. 

Lại có f(3) là giá trị của hàm số tại x = 3, quan sát đồ thị ta thấy x = 3 thì y = 0 (do điểm có tọa độ (3; 0) thuộc đồ thị hàm số) nên f(3) = 0. 

Vậy f(0) = – 1; f(3) = 0. 

c) Điểm thuộc đồ thị có tung độ bằng 0 hay y = 0 chính là điểm có tọa độ (3; 0). 

Bài 6 trang 38 Toán lớp 10 Tập 1: Cho hàm số $y=\frac{1}{x}$. Chứng tỏ hàm số đã cho: 

a) Nghịch biến trên khoảng (0; + ∞);

b) Nghịch biến trên khoảng (– ∞; 0).

Lời giải:

Ta có: $y=f\left(x\right)=\frac{1}{x}$.

Tập xác định của hàm số đã cho: D = $ℝ\backslash \left\{0\right\}$.

a) Lấy hai giá trị x₁, x₂ tùy ý thuộc khoảng (0; + ∞) sao cho 0 < x₁ < x₂.

Khi đó $\frac{1}{x_1}>\frac{1}{x_2}$ hay f(x₁) > f(x₂).

Vậy hàm số đã cho nghịch biến trên khoảng (0; + ∞).

b) Lấy hai giá trị x₁, x₂ tùy ý thuộc khoảng (– ∞; 0) sao cho x₁ < x₂ < 0.

Khi đó $\frac{1}{x_1}>\frac{1}{x_2}$ hay f(x₁) > f(x₂).

Vậy hàm số đã cho nghịch biến trên khoảng (– ∞; 0).

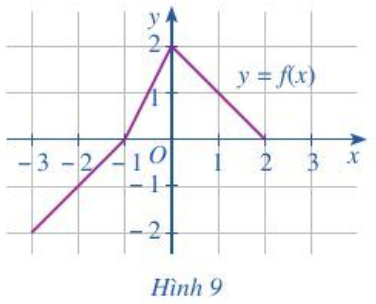
Bài 7 trang 38 Toán lớp 10 Tập 1: Cho hàm số y = f(x) có đồ thị như Hình 9.

Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số y = f(x).

Lời giải:

Quan sát đồ thị hàm số y = f(x) ở Hình 9, ta thấy:

+ Đồ thị hàm số “đi lên” (theo chiều từ trái qua phải) trong các khoảng (– 3; – 1) và (– 1; 0) nên hàm số đã cho đồng biến trên các khoảng (– 3; – 1) và (– 1; 0). 

+ Đồ thị hàm số “đi xuống” (theo chiều từ trái qua phải) trong khoảng (0; 2) nên hàm số đã cho nghịch biến trên khoảng (0; 2). 

Bài 8 trang 38 Toán lớp 10 Tập 1: Một lớp muốn thuê một chiếc xe khách cho chuyến tham quan với tổng đoạn đường cần di chuyển trong khoảng từ 550 km đến 600 km, có hai công ty được tiếp cận để tham khảo giá.

Công ty A có giá khởi đầu là 3,75 triệu đồng cộng thêm 5 000 đồng cho mỗi ki-lô-mét chạy xe. 

Công ty B có giá khởi đầu là 2,5 triệu đồng cộng thêm 7 500 đồng cho mỗi ki-lô-mét chạy xe. Lớp đó nên chọn công ty nào để chi phí là thấp nhất? 

Lời giải:

Ta có: 3,75 triệu đồng = 3 750 000 đồng; 2,5 triệu đồng = 2 500 000 đồng. 

Gọi x (km) là tổng đoạn đường cần di chuyển của lớp. 

Theo bài ra ta có: 550 ≤ x ≤ 600. 

Giả sử y (đồng) là số tiền phải trả để thuê xe. 

Khi đó đối với từng xe của mỗi công ty, ứng với mỗi giá trị của x có đúng một giá trị của y nên y là hàm số của x. 

Đối với công ty A, ta có số tiền cần trả được biểu diễn theo hàm số:  

y_A = 3 750 000 + 5000x 

Đối với công ty B, ta có số tiền cần trả được biểu diễn theo hàm số:  

y_B = 2 500 000 + 7500x 

Ta cần so sánh y_A và y_B với điều kiện của x là 550 ≤ x ≤ 600 để chọn ra công ty có chi phí thấp nhất. 

Ta có: y_A = 3 750 000 + 5000x = (2 500 000 + 5000x) + 1 250 000

y_B = 2 500 000 + 7500x = (2 500 000 + 5000x) + 2500x

Do 550 ≤ x ≤ 600 ⇔ 550 . 2500 ≤ 2500x ≤ 600 . 2500 

⇔ 1 375 000 ≤ 2500x ≤ 1 500 000

Mà 1 250 000 < 1 375 000

Do đó (2 500 000 + 5000x) + 1 250 000 < (2 500 000 + 5000x) + 2500x 

Hay y_A < y_B với 550 ≤ x ≤ 600. 

Vậy để chi phí là thấp nhất thì lớp đó nên chọn xe của công ty A. 

Lời giải bài tập Toán lớp 10 Bài 1: Hàm số và đồ thị Cánh diều hay khác:

• Giải Toán 10 trang 31 Tập 1
• Giải Toán 10 trang 32 Tập 1
• Giải Toán 10 trang 33 Tập 1
• Giải Toán 10 trang 34 Tập 1
• Giải Toán 10 trang 35 Tập 1
• Giải Toán 10 trang 36 Tập 1
• Giải Toán 10 trang 37 Tập 1