Giải Toán 10 trang 63 Tập 1 Cánh diều

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 63 Tập 1 trong Bài 1: Giá trị lượng giác của một góc từ 0 đến 180. Định lý côsin và định lý sin trong tam giác Toán lớp 10 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 63.

Giải Toán 10 trang 63 Tập 1 Cánh diều

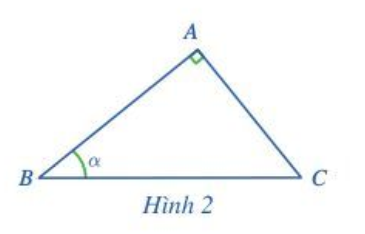
Hoạt động 1 trang 63 Toán lớp 10 Tập 1: Cho tam giác ABC vuông tại A có $\widehat{ABC}=\alpha$ (Hình 2). ....

a) Nhắc lại định nghĩa sin α, cos α, tan α, cot α. 

b) Biểu diễn tỉ số lượng giác của góc 90° – α theo tỉ số lượng giác của góc α. 

Lời giải:

a) Tam giác ABC vuông tại A có $\widehat{ABC}=\alpha$. Khi đó ta có: 

$\sin \alpha =\frac{AC}{BC},\cos \alpha =\frac{AB}{BC},\tan \alpha =\frac{AC}{AB},\cot \alpha =\frac{AB}{AC}$

b) Xét tam giác ABC vuông tại A, ta có:

$\sin \widehat{ACB}=\frac{AB}{BC}$

Ta lại có: $\widehat{ABC}+\widehat{ACB}=90°$ (hai góc phụ nhau).

Nên $\widehat{ACB}=90°-\widehat{ABC}=90°-\alpha$

Mặt khác: $\cos \alpha =\frac{AB}{BC}$

⇒ sin(90° – α) = cos α;

cos(90° – α) = sin α;

tan(90° – α) = cot α;

cot(90° – α) = tan α. 

Hoạt động 2 trang 63 Toán lớp 10 Tập 1:

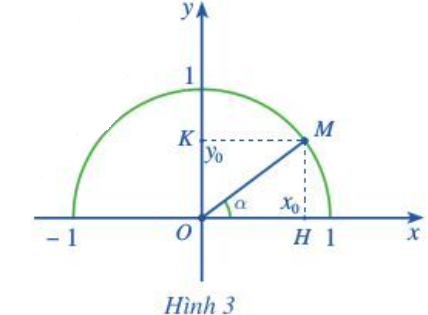
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O nằm phía trên trục hoành bán kính R = 1 được gọi là nửa đường tròn đơn vị (Hình 3). Với mỗi góc nhọn α ta có thể xác định một điểm M duy nhất trên nửa đường tròn đơn vị sao cho $\widehat{xOM}=\alpha$. Giả sử điểm M có tọa độ (x₀; y₀). Hãy tính sin α, cos α, tan α, cot α theo x₀, y_­0.

Lời giải:

Để tính sin α, cos α, tan α, cot α theo x₀, y_­0, ta làm như sau: 

Xét tam giác OMH vuông tại H, ta có: 

$\sin \alpha =\frac{MH}{OM}=\frac{y_0}{1}=y_0,\cos \alpha =\frac{OH}{OM}=\frac{x_0}{1}=x_0,$

$\tan \alpha =\frac{MH}{OH}=\frac{y_0}{x_0},\cot \alpha =\frac{OH}{MH}=\frac{x_0}{y_0}$.

Lời giải bài tập Toán lớp 10 Bài 1: Giá trị lượng giác của một góc từ 0⁰ đến 180⁰. Định lý côsin và định lý sin trong tam giác Cánh diều hay khác:

• Giải Toán 10 trang 62 Tập 1
• Giải Toán 10 trang 64 Tập 1
• Giải Toán 10 trang 66 Tập 1
• Giải Toán 10 trang 67 Tập 1
• Giải Toán 10 trang 68 Tập 1
• Giải Toán 10 trang 69 Tập 1
• Giải Toán 10 trang 70 Tập 1
• Giải Toán 10 trang 71 Tập 1