Giải Toán 10 trang 68 Tập 1 Cánh diều

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 68 Tập 1 trong Bài 1: Giá trị lượng giác của một góc từ 0 đến 180. Định lý côsin và định lý sin trong tam giác Toán lớp 10 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 68.

Giải Toán 10 trang 68 Tập 1 Cánh diều

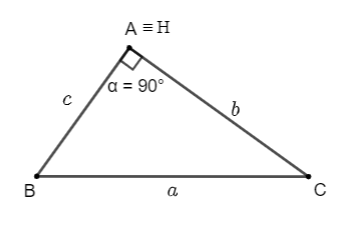
Hoạt động 8 trang 68 Toán lớp 10 Tập 1: Cho tam giác ABC có BC = a, AC = b, $\widehat{BAC}=\alpha$ . Kẻ đường cao BH.

Cho α là góc vuông. Chứng minh a² = b² + c² – 2bc cos α. 

Lời giải:

Do α = 90° ⇒ cos α = cos 90° = 0 

⇒ 2bc cos α = 2 bc cos 90° = 0

Tam giác ABC vuông tại A (do α = 90°), áp dụng định lí Pythagore ta có:

BC² = AB² + AC² = c² + b² – 0 = b² + c² – 2bc cos α.

Vậy a² = b² + c² – 2bc cos α.

Luyện tập 2 trang 68 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 5, AC = 6, BC = 7. Tính cos A.

Lời giải:

Áp dụng định lí côsin trong tam giác ABC ta có: 

BC² = AB² + AC² – 2 AB . AC . cos A

$\Rightarrow cosA=\frac{A{B}^2+A{C}^2-B{C}^2}{2AB.AC}$

Thay số vào ta được: $\cos A=\frac{5^2+6^2-7^2}{\mathrm{2.5.6}}=\frac{1}{5}=0,2$.

Vậy cos A = 0,2.  

Lời giải bài tập Toán lớp 10 Bài 1: Giá trị lượng giác của một góc từ 0⁰ đến 180⁰. Định lý côsin và định lý sin trong tam giác Cánh diều hay khác:

• Giải Toán 10 trang 62 Tập 1
• Giải Toán 10 trang 63 Tập 1
• Giải Toán 10 trang 64 Tập 1
• Giải Toán 10 trang 66 Tập 1
• Giải Toán 10 trang 67 Tập 1
• Giải Toán 10 trang 69 Tập 1
• Giải Toán 10 trang 70 Tập 1
• Giải Toán 10 trang 71 Tập 1