Tam giác ABC vuông tại A có AB = AC = 30cm. Hai đường trung tuyến BF và CE
Câu hỏi:
Tam giác ABC vuông tại A có AB = AC = 30cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích tam giác GFC bằng:
A.
B.
C.
D.
Trả lời:
Đáp án đúng là: C
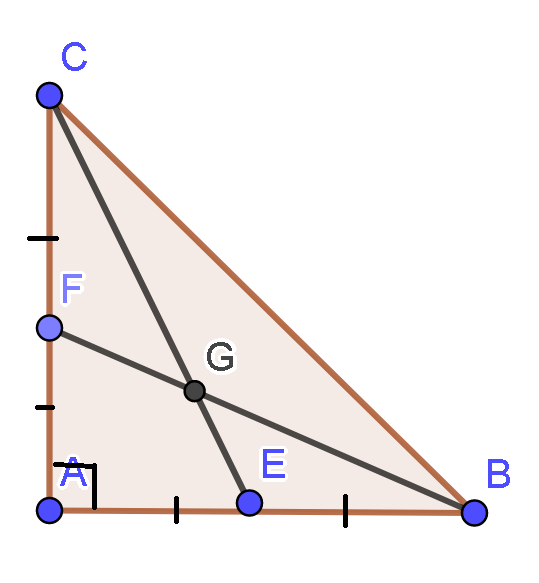
Vì F là trung điểm của AC
Đường thẳng BF cắt CE tại G suy ra G là trọng tâm tam giác ABC.
Khi đó:
Vậy diện tích tam giác GFC là:

