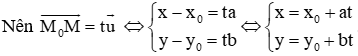Hoạt động 2 trang 74 Toán lớp 10 Tập 2 Cánh diều
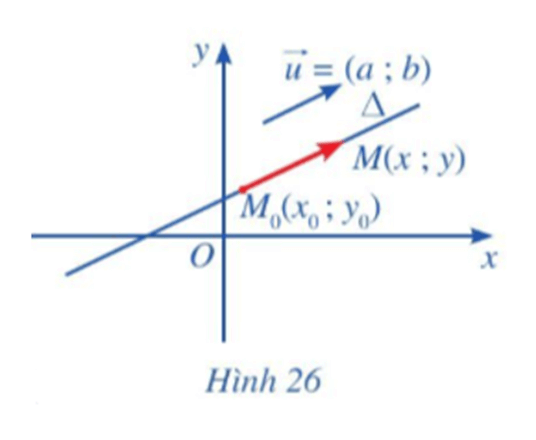
Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ đi qua điểm M(x; y) và có vectơ chỉ phương . Xét điểm M(x; y) nằm trên ∆ (Hình 26).
Giải Toán lớp 10 Bài 3: Phương trình đường thẳng
Hoạt động 2 trang 74 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ đi qua điểm M0(x0; y0) và có vectơ chỉ phương →u=(a;b). Xét điểm M(x; y) nằm trên ∆ (Hình 26).
a) Nhận xét về phương của hai vectơ →u và →M0M.
b) Chứng minh có số thực t sao cho →M0M=t→u.
c) Biểu diễn tọa độ của điểm M qua tọa độ của điểm M0 và tọa độ của vectơ chỉ phương →u.
Lời giải:
a) Đường thẳng ∆ đi qua điểm M0 và M, nên đường thẳng ∆ chính là đường thẳng MM0. Khi đó vectơ →M0M có giá chính là đường thẳng ∆.
Vectơ →u là vectơ chỉ phương của đường thẳng ∆ nên giá của vectơ →u phải song song hoặc trùng với đường thẳng ∆.
Do đó, hai vectơ →u và →M0M có giá song song hoặc trùng nhau.
Vậy hai vectơ →u và →M0M cùng phương.
b) Theo câu a, hai vectơ →u và →M0M cùng phương nên có số thực t sao cho →M0M=t→u.
c) Ta có: →M0M=(x−x0;y−y0),→u=(a;b).
Lời giải Toán 10 Bài 3: Phương trình đường thẳng hay, chi tiết khác:
Hoạt động 1 trang 73 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ....
Luyện tập 1 trang 75 Toán lớp 10 Tập 2: : Cho đường thẳng Δ có phương trình tham số ....
Hoạt động 3 trang 75 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ....
Hoạt động 4 trang 75 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ....
