∆ABC có AB = căn bậc hai của 6 - căn bậc hai của 2 /2, BC = căn bậc hai của 3, CA = căn bậc hai của 2. Gọi D là chân đường phân giác trong của góc A. Khi đó số đo của góc ADB bằng: A. 45°; B

Hướng dẫn giải

Đáp án đúng là: C

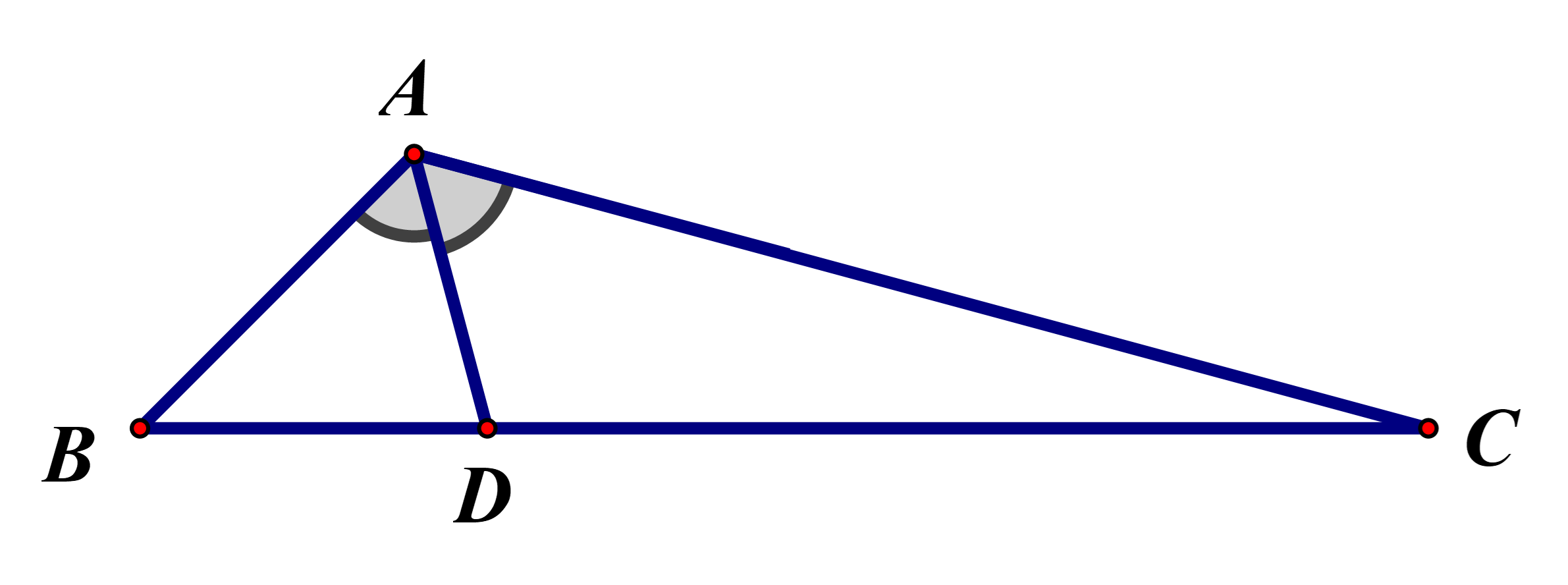
Áp dụng hệ quả của định lí côsin cho ∆ABC, ta có:

⦁ \(\cos \widehat {BAC} = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}} = \frac{{2 - \sqrt 3 + 2 - 3}}{{2.\frac{{\sqrt 6 - \sqrt 2 }}{2}.\sqrt 2 }} = - \frac{1}{2}\).

Suy ra \(\widehat {BAC} = 120^\circ \).

⦁ \(\cos \widehat {ABC} = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}} = \frac{{2 - \sqrt 3 + 3 - 2}}{{2.\frac{{\sqrt 6 - \sqrt 2 }}{2}.\sqrt 3 }} = \frac{{\sqrt 2 }}{2}\).

Suy ra \(\widehat {ABC} = 45^\circ \) hay \(\widehat {ABD} = 45^\circ \).

Ta có AD là tia phân giác của \(\widehat {BAC}\).

Suy ra \(\widehat {BAD} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}.120^\circ = 60^\circ \).

∆ABD có: \(\widehat {BAD} + \widehat {ABD} + \widehat {ADB} = 180^\circ \) (định lí tổng ba góc của một tam giác)

\( \Leftrightarrow \widehat {ADB} = 180^\circ - \left( {\widehat {BAD} + \widehat {ABD}} \right) = 180^\circ - \left( {60^\circ + 45^\circ } \right) = 75^\circ \).

Vậy \(\widehat {ADB} = 75^\circ \).

Do đó ta chọn phương án C.