Biết rằng hàm số y = f(x) = x3 + 2x + 1 đồng biến trên ℝ. Đặt A = x^2+ 3/x^2 + 1)^3 + 2 x^2 + 3/x^2 + 1 và B = 8/( x^2 + 1)^3 + 4/x^2 + 1. Khẳng định nào sau đây đúng? A. A > B; B. A = B;
Câu hỏi:
Biết rằng hàm số y = f(x) = x3 + 2x + 1 đồng biến trên ℝ. Đặt \(A = {\left( {\frac{{{x^2} + 3}}{{{x^2} + 1}}} \right)^3} + 2\left( {\frac{{{x^2} + 3}}{{{x^2} + 1}}} \right)\) và \(B = \frac{8}{{{{\left( {{x^2} + 1} \right)}^3}}} + \frac{4}{{{x^2} + 1}}\). Khẳng định nào sau đây đúng?
A. A > B;
B. A = B;
C. A < B;
D. A ≤ B.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: A
Ta có \(B = \frac{8}{{{{\left( {{x^2} + 1} \right)}^3}}} + \frac{4}{{{x^2} + 1}} = {\left( {\frac{2}{{{x^2} + 1}}} \right)^3} + 2.\frac{2}{{{x^2} + 1}}\).
Ta đặt \({x_1} = \frac{2}{{{x^2} + 1}}\) và \({x_2} = \frac{{{x^2} + 3}}{{{x^2} + 1}}\).
Ta có \[{x_2} = \frac{{{x^2} + 3}}{{{x^2} + 1}} = \frac{{{x^2} + 1 + 2}}{{{x^2} + 1}} = \frac{{{x^2} + 1}}{{{x^2} + 1}} + \frac{2}{{{x^2} + 1}} = 1 + \frac{2}{{{x^2} + 1}} > \frac{2}{{{x^2} + 1}}\].
Ta suy ra x2 > x1 hay x1 < x2.
Vì hàm số đã cho đồng biến trên ℝ và x1 < x2 nên ta có f(x1) < f(x2).
Suy ra \({\left( {\frac{2}{{{x^2} + 1}}} \right)^3} + 2.\frac{2}{{{x^2} + 1}} + 1 < {\left( {\frac{{{x^2} + 3}}{{{x^2} + 1}}} \right)^3} + 2.\frac{{{x^2} + 3}}{{{x^2} + 1}} + 1\).
Do đó \({\left( {\frac{2}{{{x^2} + 1}}} \right)^3} + 2.\frac{2}{{{x^2} + 1}} < {\left( {\frac{{{x^2} + 3}}{{{x^2} + 1}}} \right)^3} + 2.\frac{{{x^2} + 3}}{{{x^2} + 1}}\).
Vì vậy B < A hay A > B.
Vậy ta chọn phương án A.
Xem thêm bài tập trắc nghiệm Toán 10 CTST có lời giải hay khác:
Câu 1:
Cho parabol y = ax2 + bx + 4 có trục đối xứng là đường thẳng \(x = \frac{1}{3}\) và đi qua điểm A(1; 3). Tổng giá trị a + 2b bằng:
Xem lời giải »
Câu 2:
Cho hàm số f(x) = ax2 + bx + c (a, b, c ≠ 0) có đồ thị như hình vẽ bên.
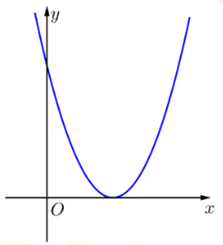
Biết f(c) = c. Giá trị của b là:
Xem lời giải »
Câu 3:
Biết rằng hàm số y = ax2 + bx + c (a ≠ 0) đạt giá trị nhỏ nhất bằng 4 tại x = 2 và có đồ thị đi qua điểm A(0; 6). Giá trị biểu thức P = abc bằng
Xem lời giải »
Câu 4:
Cho hàm số \(y = f\left( x \right) = \frac{{x + 2}}{{{x^2} + 1}}\). Gọi (C) là đồ thị của hàm số đã cho và điểm M(m + 1; 1). Giá trị của tham số m để điểm M nằm trên đồ thị (C) là:
Xem lời giải »
Câu 5:
Một cửa hàng buôn giày nhập một đôi với giá là 40 USD. Cửa hàng ước tính rằng nếu đôi giày được bán với giá x USD thì mỗi tháng khách hàng sẽ mua (120 – x) đôi. Hỏi cửa hàng bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất?
Xem lời giải »
Câu 6:
Dây truyền đỡ trên cầu treo có dạng parabol ACB như hình vẽ. Đầu, cuối của dây được gắn vào các điểm A, B trên mỗi trục AA’ và BB’ với độ cao 30 m. Chiều dài A’B’ trên nền cầu bằng 200 m. Gọi Q’, P’, H’, C’, I’, J’, K’ là các điểm chia đoạn A’B’ thành các phần bằng nhau (C’ chia đoạn A’B’ thành hai phần bằng nhau). Các thanh thẳng đứng nối nền cầu với đáy dây truyền: QQ’, PP’, HH’, CC’, II’, JJ’, KK’ gọi là các dây cáp treo.
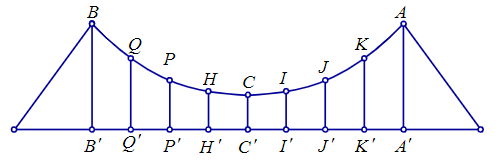
Biết độ cao ngắn nhất của dây truyền trên cầu là C’C = 5 m. Tổng độ dài của các dây cáp treo là:
Xem lời giải »
Câu 7:
Khi nuôi cá thí nghiệm trong hồ, một nhà sinh học phát hiện ra rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ có cân nặng P(n) = 360 – 10n. Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích để trọng lượng cá sau một vụ thu được nhiều nhất?
Xem lời giải »
Câu 8:
Một chiếc cổng hình parabol có phương trình \(y = - \frac{1}{2}{x^2}\). Biết cổng có chiều rộng d = 5 m. Chiều cao h của cổng bằng:
Xem lời giải »



