Cho f(x) = ax^2 + bx + c (a khác 0) có đồ thị đi qua ba điểm (0; 1); (1; –2); (3; 5)

Cho f(x) = ax² + bx + c (a ≠ 0) có đồ thị đi qua ba điểm (0; 1); (1; –2); (3; 5). Kết luận nào sau đây đúng?

A. f(x) âm trong khoảng $\left(\frac{1}{4};3\right)$;

B. f(x) âm trong khoảng $\left(-\infty ;\frac{1}{4}\right)$;                

Hướng dẫn giải

Đáp án đúng là: A

Xét f(x) = ax² + bx + c (a ≠ 0):

⦁ Ta có đồ thị đi qua điểm (0; 1) nên f(0) = 1.

Khi đó a.0² + b.0 + c = 1.

Vì vậy c = 1.

⦁ Ta có đồ thị đi qua điểm (1; –2) nên f(1) = –2.

Khi đó a.1² + b.1 + c = –2.

Vì vậy a + b + c = –2 (1)

Thế c = 1 vào (1) ta được a + b + 1 = –2.

Do đó a = –b – 3.

⦁ Ta có đồ thị đi qua điểm (3; 5) nên f(3) = 5.

Khi đó a.3² + b.3 + c = 5.

Vì vậy 9a + 3b + c = 5 (2)

Thế c = 1 và a = –b – 3 vào (2) ta được 9(–b – 3) + 3b + 1 = 0.

Suy ra –9b – 27 + 3b + 1 = 0.

Do đó –6b – 26 = 0.

Vì vậy $b=-\frac{13}{3}$.

Với $b=-\frac{13}{3}$, ta có a = –b – 3 = $\frac{13}{3}-3=\frac{4}{3}$ > 0.

Vậy ta có tam thức bậc hai $f\left(x\right)=\frac{4}{3}{x}^2-\frac{13}{3}x+1$.

Ta có ∆ = ${\left(-\frac{13}{3}\right)}^2-4.\frac{4}{3}.1=\frac{121}{9}$ > 0.

Suy ra f(x) có 2 nghiệm phân biệt là:

Ta có bảng xét dấu của f(x) như sau:

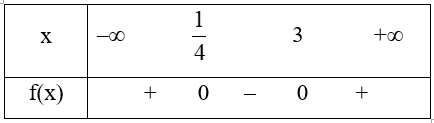
Vậy f(x) âm trong khoảng $\left(\frac{1}{4};3\right)$ và f(x) dương trong hai khoảng $\left(-\infty ;\frac{1}{4}\right)$ và (3; +∞).

Ta chọn phương án A.