Giải Toán 10 trang 20 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 20 Tập 1 trong Bài 2: Tập hợp Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 20.

Giải Toán 10 trang 20 Tập 1 Chân trời sáng tạo

Vận dụng trang 20 Toán lớp 10 Tập 1: Bạn An khẳng định rằng: Với các tập hợp A, B, C bất kì, nếu A ⊂ B và B ⊂ C thì A ⊂ C. Khẳng định của bạn An có đúng không? Hãy giải thích bằng cách sử dụng biểu đồ ven.

Lời giải:

Khẳng định của bạn An là đúng.

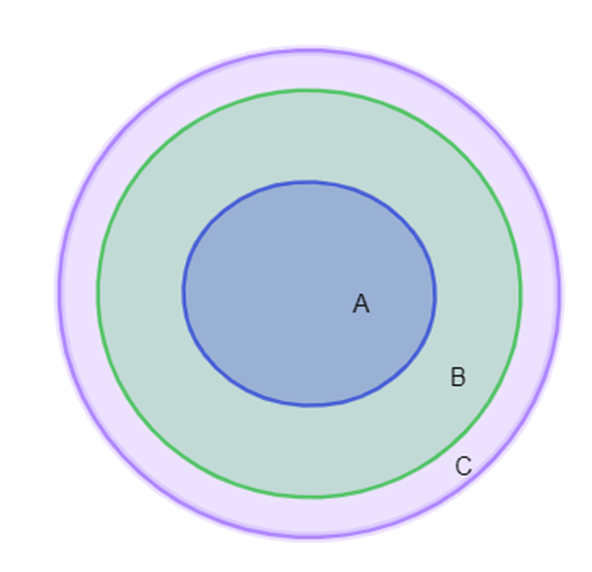
Thật vậy, ta có sơ đồ ven sau:

Dựa vào sơ đồ ta thấy tập hợp A nằm trong tập hợp B và tập hợp B nằm trong tập hợp C. Do đó tập hợp A nằm hoàn toàn trong tập hợp C hay tất cả phần tử của tập hợp A đều thuộc tập hợp C.

Suy ra A ⊂ C.

Thực hành 6 trang 20 Toán lớp 10 Tập 1: Dùng các kí hiệu đoạn, khoảng, nửa khoảng để viết các tập hợp sau đây:

a) $\left\{x\in ℝ|-2<x<3\right\};$

b) $\left\{x\in ℝ|1\le x\le 10\right\};$

c) $\left\{x\in ℝ|-5<x\le \sqrt{3}\right\};$

d) $\left\{x\in ℝ|\pi \le x<4\right\};$

e) $\left\{x\in ℝ|x<\frac{1}{4}\right\};$

g) $\left\{x\in ℝ|x\ge \frac{\pi }{2}\right\}.$

Lời giải:

a) $\left\{x\in ℝ|-2<x<3\right\}=\left(-2;3\right).$

b) $\left\{x\in ℝ|1\le x\le 10\right\}=\left[1;10\right].$

c) $\left\{x\in ℝ|-5<x\le \sqrt{3}\right\}=\left(-5;\sqrt{3}\right].$

d) $\left\{x\in ℝ|\pi \le x<4\right\}=\left[\pi ;4\right).$

e) $\left\{x\in ℝ|x<\frac{1}{4}\right\}=\left(-\infty ;\frac{1}{4}\right).$

g) $\left\{x\in ℝ|x\ge \frac{\pi }{2}\right\}=\left[\frac{\pi }{2};+\infty \right).$

Bài 1 trang 20 Toán lớp 10 Tập 1: Viết các tập hợp sau đây dưới dạng liệt kê các phần tử:

a) A = {x ∈ ℤ| |x| < 5};

b) B = {x ∈ ℝ| 2x² – x – 1 = 0};

c) C = {x ∈ ℕ | x có hai chữ số}.

Lời giải:

a) A = {x ∈ ℤ | |x| < 5}

Xét |x| < 5

⇔ x < 5 hoặc – x < 5

⇔ x < 5 hoặc x > - 5

Suy ra -5 < x < 5.

Mà x ∈ ℤ nên x ∈ {-4; -3; -2; -1; 0; 1; 2; 3; 4}.

Vậy A = {-4; -3; -2; -1; 0; 1; 2; 3; 4}.

b) Xét phương trình 2x² – x – 1 = 0

⇔ (x – 1)(2x + 1) = 0

$\iff \left[\begin{array}{l}x-1=0\\ 2x+1=0\end{array}\right.$

Mà 1;  $\frac{1}{2}\in ℝ$

Vậy B = $\left\{1;\frac{1}{2}\right\}$

c) Các số tự nhiên có hai chữ số là 10; 11; 12; 13; 14; 15; …; 99.

Vậy C = {10; 11; 12; 13; 14; 15; …; 99}.

Lời giải bài tập Toán lớp 10 Bài 2: Tập hợp Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 16

• Giải Toán 10 trang 18

• Giải Toán 10 trang 19

• Giải Toán 10 trang 21