Giải Toán 10 trang 57 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 57 Tập 1 trong Bài 2: Hàm số bậc hai Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 57.

Giải Toán 10 trang 57 Tập 1 Chân trời sáng tạo

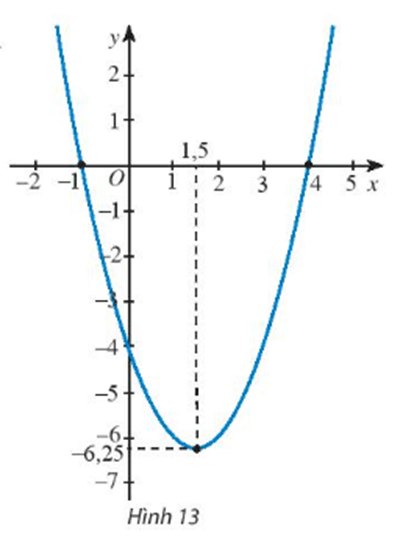
Bài 8 trang 57 Toán lớp 10 Tập 1: Tìm công thức của hàm số bậc hai có đồ thị như Hình 13.

Lời giải:

Dựa vào hình vẽ ta thấy:

Đồ thị hàm số có dạng parabol nên hàm số có dạng  y = ax² + bx + c với a, b, c ∈  và a ≠ 0. Hơn nữa đồ thị hàm số có bề lõm hướng lên trên nên a > 0.

Đồ thị hàm số cắt trục tung tại điểm tọa độ (0; -4) nên ta có:  4 = a.0² + b.0 + c ⇔ c = 4.

Điểm đỉnh S của đồ thị hàm số có tọa độ x_S = 1,5 và y_S = -6.25

$\Rightarrow x_S=-\frac{b}{2a}=1,5\iff b=-3a$

Đồ thị hàm số cắt trục hoành tại hai điểm (-1; 0) và (4; 0) nên thay x = -1 và y = 0 vào hàm số ta được: 0 = a(-1)² + b(-1) + c

⇔ 0 = a – b + c

Mà b = – 3a và c = 4 nên ta có: a + 3a + 4 = 0 ⇔ a = 1 ⇒ b = -3.

Vậy hàm số cần tìm là  y = x² – 3x + 4.

Bài 9 trang 57 Toán lớp 10 Tập 1: Chiếc cầu dây văng một nhịp được thiết kế hai bên thành cầu có dạng parabol và được cố định bằng các dây cáp song song.

Dựa vào bản vẽ ở Hình 14, hãy tính chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên. Biết:

- Dây dài nhất là 5m, dây ngắn nhất là 0,8m. Khoảng cách giữa các dây bằng nhau.

- Nhịp cầu dài 30m.

- Cần tính thêm 5% chiều dài mỗi sợi dây cáp để neo cố định.

Lời giải:

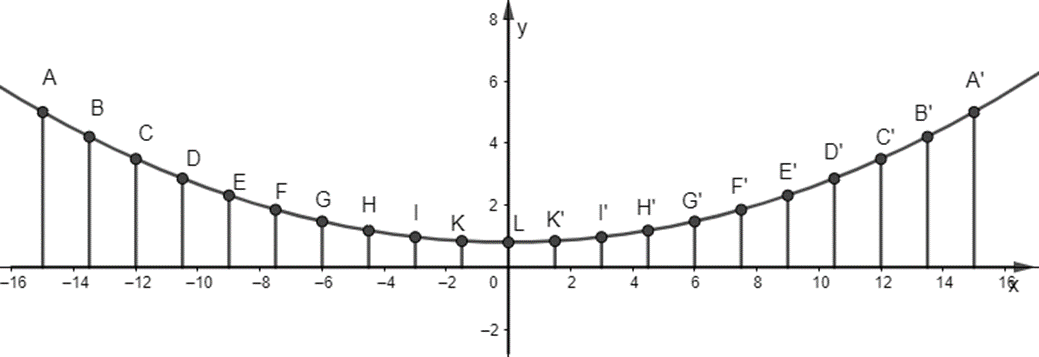
Hình dây văng có dạng parabol, nên ta có hình vẽ sau:

Độ dài của dây cáp tương ứng với tung độ của các điểm A, B, C, D, E, F, G, H, I, K, L, K’, I’, H’, G’, F’, E’, D’, C’, B’, A’.

Dây dài nhất tương ứng với điểm A và A’ trên đồ thị. Khi đó A(-15; 5) và A’(15; 5).

Dây ngắn nhất trên đồ thị tương ứng với điểm L trên đồ thị. Khi đó L(0; 0,8).

Gọi hàm số đi qua các điểm này có dạng y = ax² + bx + c.

Ta có hàm số đi qua A(-15; 5) nên thay x = -15 và y = 5 ta có: 225a – 15b + c = 5;

Ta có hàm số đi qua A(15; 5) nên thay x = 15 và y = 5 ta có: 225a + 15b + c = 5;

Ta có hàm số đi qua điểm L(0; 1) nên thay x = 0 và y = 1 ta có: b + c = 1;

Khi đó ta có hệ phương trình: $\left\{\begin{array}{l}225a-15b+c=5\\ 225a+15b+c=5\\ c=1\end{array}\right.\iff \left\{\begin{array}{l}a=\frac{4}{225}\\ b=0\\ c=1\end{array}\right.$

Suy ra ta có hàm số y = $\frac{4}{225}$x² + 1.

Hàm số có trục đối xứng là x = 0 hay chính là trục tung. Do đó các điểm A, B, C, D, E, F, G, H, I, K đối xứng với các điểm A’, B’, C’, D’, E’, F’, G’, H’, I’, K’ qua trục tung. Vì thế các điểm này có cùng tung độ.

Vì nhịp cầu dài 30 m nên khoảng cách giữa các dây cáp là: 30: 20 = 1,5 m.

Do đó hoành độ các điểm K’, I’, H’, G’, F’, E’, D’, C’, B’, A’ lần lượt là:

x_K’ = 1,5 ⇒ y_K’ = $\frac{26}{25}$ ⇒ K’$\left(\frac{3}{2};\frac{26}{25}\right)$. Do đó độ dài dây cáp ở điểm K và K’ là $\frac{26}{25}$.

x_I’ = 3 ⇒ y_I’ = $\frac{29}{25}$  ⇒ I’$\left(3;\frac{29}{25}\right)$. Do đó độ dài dây cáp ở điểm I và I’ là  $\frac{29}{25}$.

x_H’ = 4,5 ⇒ y_H’ = $\frac{34}{25}$  ⇒ H’$\left(\frac{9}{2};\frac{34}{25}\right)$. Do đó độ dài dây cáp ở điểm H và H’ là $\frac{34}{25}$.

x_G’ = 6 ⇒ y_G’ = $\frac{41}{25}$ ⇒ G’ $\left(6;\frac{41}{25}\right)$. Do đó độ dài dây cáp ở điểm G và G’ là $\frac{41}{25}$.

x_F’ = 7,5 ⇒ y_F’ = 2 ⇒ F’$\left(\frac{15}{2};2\right)$. Do đó độ dài dây cáp ở điểm F và F’ là 2.

x_E’ = 9 ⇒ y_E’ = $\frac{61}{25}$ ⇒ E’$\left(9;\frac{61}{25}\right)$. Do đó độ dà.i dây cáp ở điểm E và E’ là $\frac{61}{25}$ .

x_D’ = 10,5 ⇒ y_D’ =  $\frac{74}{25}$ ⇒ D’$\left(\frac{21}{2};\frac{74}{25}\right)$. Do đó độ dài dây cáp ở điểm D và D’ là $\frac{74}{25}$ .

x_C’ = 12 ⇒ y_C’ = $\frac{89}{25}$  ⇒ C’$\left(12;\frac{89}{25}\right)$. Do đó độ dài dây cáp ở điểm H’ là $\frac{89}{25}$ .

x_B’ = 13,5 ⇒ y_B’ = $\frac{106}{25}$ ⇒ B’$\left(\frac{27}{2};\frac{106}{25}\right)$. Do đó độ dài dây cáp ở điểm B và B’ là $\frac{106}{25}$.

x_A’ = 15 ⇒ y_A’ = 5 ⇒ A’. Do đó độ dài dây cáp ở điểm A và A’ là 5.

Vì cần tính thêm 5% chiều dài mỗi sợi dây cap để neo cố định nên tổng độ dài các dây cáp là:

$2.\left(\frac{26}{25}+\frac{29}{25}+\frac{34}{25}+\frac{41}{25}+2+\frac{61}{25}+\frac{74}{25}+\frac{89}{25}+\frac{106}{25}+5\right)+2.\left(\frac{26}{25}+\frac{29}{25}+\frac{34}{25}+\frac{41}{25}+2+\frac{61}{25}+\frac{74}{25}+\frac{89}{25}+\frac{106}{25}+5\right).0,5\%=\frac{2667}{50}m$

Vậy tổng độ dài dây cáp cần dùng $\frac{2667}{50}m.$

Lời giải bài tập Toán lớp 10 Bài 2: Hàm số bậc hai Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 49

• Giải Toán 10 trang 52

• Giải Toán 10 trang 53

• Giải Toán 10 trang 55

• Giải Toán 10 trang 56