Giải Toán 10 trang 61 Tập 1 Chân trời sáng tạo

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 61 Tập 1 trong Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 61.

Giải Toán 10 trang 61 Tập 1 Chân trời sáng tạo

Hoạt động khởi động trang 61 Toán lớp 10 Tập 1: Làm thế nào để mở rộng khái niệm tỉ số lượng giác của góc nhọn cho các góc từ 0° đến 180°?

Lời giải:

Để mở rộng khái niệm tỉ số lượng giác của góc nhọn cho góc từ 0° đến 180° ta thực hiện như sau:

Với mỗi góc α (0° ≤ α ≤ 180°) ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho $\widehat{xOM}=\alpha$. Gọi (x₀; y₀) là tọa độ của điểm M, ta có:

+ sin của góc α là tung độ y₀  của điểm M, được kí hiệu là sinα;

+ côsin của góc α là hoành độ x₀  của điểm M, được kí hiệu là cosα;

+ tang của α là tỉ số  $\frac{y_0}{x_0}$ (x₀ ≠ 0), được kí hiệu là tanα = $\frac{y_0}{x_0}$;

+ côtang của α là tỉ số $\frac{x_0}{y_0}$ (y₀ ≠ 0), được kí hiệu là cotα = $\frac{x_0}{y_0}$ .

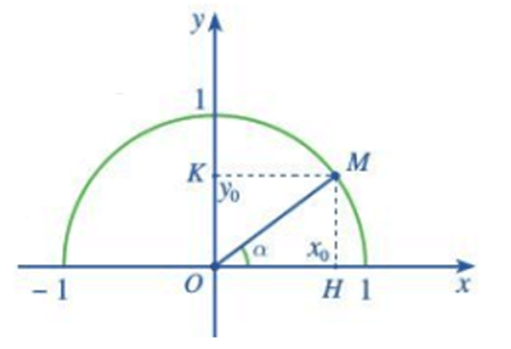
Hoạt động khám phá 1 trang 61 Toán lớp 10 Tập 1: Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn α, lấy điểm M trên nửa đường tròn đơn vị sao cho $\widehat{xOM}=\alpha$. Giả sử điểm M có tọa độ (x₀; y₀). Áp dụng cách tính tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng:

sinα = y₀; cosα = x₀ ; tanα =  $\frac{y_0}{x_0}$; cotα = $\frac{x_0}{y_0}$

Lời giải:

Trong tam giác HOM  vuông tại H có cạnh huyền OM = 1:

Ta có, sinα = sin $\widehat{HOM}$ = $\frac{MH}{OM}=\frac{y_0}{1}=y_0$ ;

cosα = cos $\widehat{HOM} =\frac{OH}{OM} = \frac{x_0}{1}=x_0$ ;

tanα = $\frac{MH}{OH}=\frac{y_0}{x_0}$ ;

cotα  =  $\frac{OH}{MH}=\frac{x_0}{y_0}$ .

Vậy sinα  = y₀; cosα  = x₀ ; tanα  =  $\frac{y_0}{x_0}$; cotα = $\frac{x_0}{y_0}$.

Lời giải bài tập Toán lớp 10 Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 62

• Giải Toán 10 trang 63

• Giải Toán 10 trang 64

• Giải Toán 10 trang 65