Giải Toán 10 trang 77 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 77 Tập 1 trong Bài 3: Giải tam giác và ứng dụng thực tế Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 77.

Giải Toán 10 trang 77 Tập 1 Chân trời sáng tạo

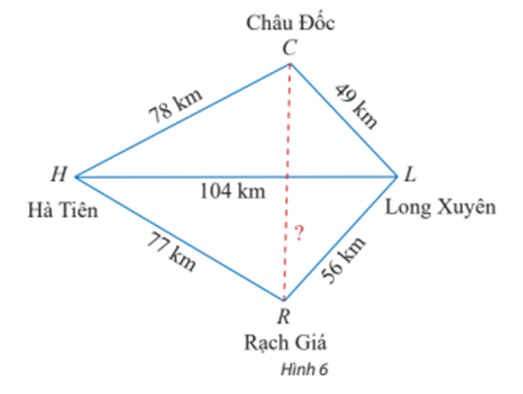
Vận dụng 2 trang 77 Toán lớp 10 Tập 1: Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố Hà Tiên, Châu Đốc, Long Xuyên, Rạch Giá là tứ giác Long Xuyên. Dựa theo các khoảng cách đã cho trên Hình 6, tính khoảng cách giữa Châu Đốc và Rạch Giá.

Lời giải:

Áp dụng hệ quả của định lí côsin cho tam giác CHL ta có:

$cos\widehat{CLH} =\frac{C{L}^2+H{L}^2-C{H}^2}{2.CL.HL}=\frac{{49}^2+{104}^2-{78}^2}{\mathrm{2.49.104}}\approx 0,6999$=

⇒$\widehat{CLH}$  ≈ 45°35'.

Áp dụng hệ quả của định lí côsin cho tam giác RHL ta có:

$cos \widehat{RLH} =\frac{R{L}^2+H{L}^2-R{H}^2}{2.RL.HL}=\frac{{56}^2+{104}^2-{77}^2}{\mathrm{2.56.104}}\approx 0,6888$

⇒ $\widehat{RLH}$ ≈ 46°28'.

Suy ra $\widehat{CLR}=\widehat{CLH}+\widehat{RLH}\approx {45}^{o}35’+{46}^{o}28’\approx {92}^{o}3\text{'}$

Áp dụng định lí côsin cho tam giác LCR ta có:

CR² = CL² + LR² – 2.CL.LR.cos$\widehat{CLR}$  = 49² + 56² – 2.49.56.cos92^o3’ ≈ 5 733,3

⇒ CR ≈ 75,7.

Vậy khoảng cách giữa Châu Đốc và Rạch Giá khoảng 75,7 km.

Bài 1 trang 77 Toán lớp 10 Tập 1: Giải tam giác ABC trong các trường hợp sau:

a) AB = 14, AC = 23, $\widehat{A}={125}^o$;

b) BC = 22, $\widehat{B}={64}^o,\widehat{C}={38}^o$;

c) AC = 22, $\widehat{B}={120}^o,\widehat{C}={28}^o$;

d) AB = 23, AC = 32, BC = 44.

Lời giải:

a) Áp dụng định lí côsin cho tam giác ABC ta có:

BC² = AB² + AC² – 2.AB.AC.cosA = 14² + 23² – 2.14.23.cos125° ≈ 1 094,4.

⇒ BC ≈ $\sqrt{1094,4}\approx 33,1$.

Áp dụng hệ quả của định lí côsin cho tam giác ABC ta có:

cosB = $\frac{A{B}^2+B{C}^2-A{C}^2}{2.AB.BC}=\frac{{14}^2+33,1^2-{23}^2}{\mathrm{2.14.33},1}\approx 0,823$  

⇒ $\widehat{B}\approx {34}^{o}37\text{'}$

Mặt khác tam giác ABC có:

$\widehat{A}+\widehat{B}+\widehat{C}={180}^o\Rightarrow \widehat{C}={180}^o-(\widehat{A}+\widehat{B})={180}^o-({125}^o+{34}^{o}37\text{'})={20}^{o}23\text{'}$

Vậy tam giác ABC có:

AB = 14, AC = 23, BC ≈ 33,1; $\widehat{A}={125}^o$; $\widehat{B}\approx {34}^{o}37\text{'}$ ; $\widehat{C}\approx {20}^{o}23\text{'}$

b) Tam giác ABC có:

$\widehat{A}+\widehat{B}+\widehat{C}={180}^o\Rightarrow \widehat{A}={180}^o-(\widehat{B}+\widehat{C})={180}^o-({64}^o+{38}^o)={78}^o$

Áp dụng định lí sin cho tam giác ABC ta có:

$\frac{BC}{\sin A}=\frac{AC}{\sin B}=\frac{AB}{\sin C}\Rightarrow \frac{22}{\sin {78}^o}=\frac{AC}{\sin {64}^o}=\frac{AB}{\sin {38}^o}$;

Suy ra: $AC=\frac{22.\sin {64}^o}{\sin {78}^o}\approx 20,2$ ; $AB=\frac{22.\sin {38}^o}{\sin {78}^o}\approx 13,8$

Vậy tam giác ABC có:

$\widehat{A}={78}^o;\widehat{B}={64}^o,\widehat{C}={38}^o$; AB ≈ 13,8; AC ≈ 20,2;  BC = 22.

c) Tam giác ABC có:

$\widehat{A}+\widehat{B}+\widehat{C}={180}^o\Rightarrow \widehat{A}={180}^o-(\widehat{B}+\widehat{C})={180}^o-({120}^o+{28}^o)={32}^o$

Áp dụng định lí sin cho tam giác ABC ta có:

Suy ra: $BC=\frac{22.\sin {32}^o}{\sin {120}^o}\approx 13,5$; $AB=\frac{22.\sin {28}^o}{\sin {120}^o}\approx 11,9$.

Vậy tam giác ABC có:

$\widehat{A}={32}^o;\widehat{B}={120}^o,\widehat{C}={28}^o$; AB ≈ 11,9; AC = 22;  BC = 13,5.

d) Áp dụng hệ quả của định lí côsin ta có:

cosA = $\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}=\frac{{23}^2+{32}^2-{44}^2}{\mathrm{2.23.32}}=\frac{-383}{1472}\approx -0,26$ ⇒ $\widehat{A}\approx {105}^{o}4\text{'}$

cosB =  $\frac{A{B}^2+B{C}^2-A{C}^2}{2.AB.BC}=\frac{{23}^2+{44}^2-{32}^2}{\mathrm{2.23.44}}=\frac{1441}{2024}\approx 0,712$ ⇒ $\widehat{B}={44}^{o}36\text{'}$

$\widehat{A}+\widehat{B}+\widehat{C}={180}^o\Rightarrow \widehat{C}={180}^o-(\widehat{A}+\widehat{B})={180}^o-({105}^{o}4\text{'}+{44}^{o}36\text{'})={30}^{o}20\text{'}$

Vậy tam giác ABC có: $\widehat{A}\approx {105}^{o}4\text{'}$; $\widehat{B}={44}^{o}36\text{'}$ ; $\widehat{C}={30}^{o}20\text{'}$ ; AB = 23, AC = 32, BC = 44.

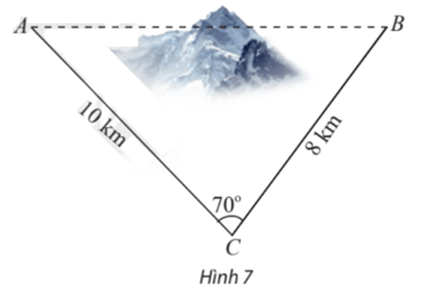
Bài 2 trang 77 Toán lớp 10 Tập 1: Để lắp đường dây điện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 10 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 8 km. Góc tạo bởi hai đoạn dây AC và CB là 70°. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B.

Lời giải:

Áp dụng định lí côsin cho tam giác ABC ta có:

AB² = AC² + BC² – 2.AC.BC.cosC = 10² + 8² – 2.10.8.cos70° ≈ 109,3

⇒ AB ≈ $\sqrt{109,3}\approx 10,5$

Ta có : (AC + CB) – AB  =(10 + 8) – 10,5  = 7,5.

Vậy vì không thể nối trực tiếp từ A đến B nên chiều dài dây tăng thêm 7,5 km.

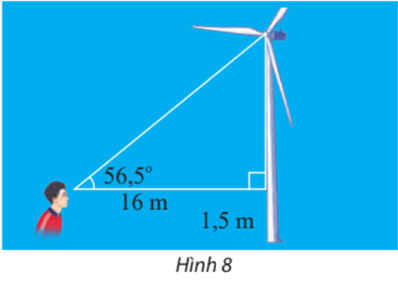
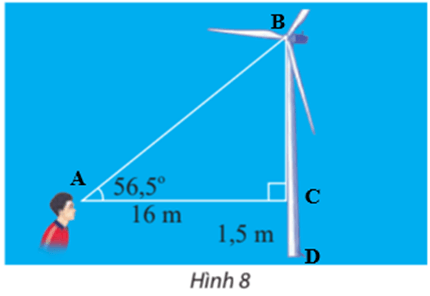
Bài 3 trang 77 Toán lớp 10 Tập 1: Một người đứng cách thân một cái quạt gió 16 m và nhìn thấy tâm của cánh quạt với góc nâng 56,5° (Hình 8). Tính khoảng cách từ tâm của cánh quạt đến mặt đất. Cho biết khoảng cách từ mắt của người đó đến mặt đất là 1,5 m.

Lời giải:

Gọi A, B, C, D lần lượt là điểm biểu diễn vị trí mắt của người quan sát, tâm cánh quạt, giao của hướng mắt nằm ngang và thân của quạt gió, vị trí chân cây quạt.

Vì tam giác ABC vuông tại C nên ta có : tanA =  $\frac{BC}{AC}=\frac{BC}{16}$

⇒ BC = 16.tan A = 16.tan56,5° ≈ 24,2 m

Do đó:  BD = BC + CD  = 24,2 + 1,5 = 25,7 m.

Vậy khoảng cách từ tâm của cánh quạt đến mặt đất khoảng 25,7 m.

Lời giải bài tập Toán lớp 10 Bài 3: Giải tam giác và ứng dụng thực tế Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 74

• Giải Toán 10 trang 75

• Giải Toán 10 trang 76

• Giải Toán 10 trang 78