Giải Toán 10 trang 93 Tập 1 Chân trời sáng tạo

❮ Bài trước Bài sau ❯

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 93 Tập 1 trong Bài 2: Tổng và hiệu của hai vectơ Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 93.

Giải Toán 10 trang 93 Tập 1 Chân trời sáng tạo

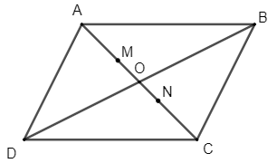
Thực hành 5 trang 93 Toán lớp 10 Tập 1: Cho hình bình hành ABCD có tâm O. Tìm ba điểm M, N, P thỏa mãn:

a) $\vec{M A} + \vec{M D} + \vec{M B} = \vec{0}$ ;

b) $\vec{N D} + \vec{N B} + \vec{N C} = \vec{0}$ ;

c) $\vec{P M} + \vec{P N} = \vec{0}$ .

Lời giải:

Cho hình bình hành ABCD có tâm O. Tìm ba điểm M, N, P thỏa mãn: vectơ MA + vectơ MD + vectơ MB = vectơ 0

a) Gọi M là trọng tâm tam giác ADB.

Khi đó ta có: $\vec{M A} + \vec{M D} + \vec{M B} = \vec{0}$

Vậy điểm M thỏa mãn $\vec{M A} + \vec{M D} + \vec{M B} = \vec{0}$ là trọng tâm của tam giác ADB.

b) Tương tự câu a, điểm N thỏa mãn $\vec{N D} + \vec{N B} + \vec{N C} = \vec{0}$ là trọng tâm của tam giác DBC.

c) ABCD là hình bình hành có tâm O nên O là giao của hai đường chéo AC và BD, đồng thời là trung điểm của mỗi đường.

Khi đó AO là đường trung tuyến của tam giác ABD nên trọng tâm M của tam giác này nằm trên cạnh AO thỏa mãn AM = $\frac{2}{3}$ AO nên OM = $\frac{1}{3}$ AO.

Và CO là đường trung tuyến của tam giác BDC nên trọng tâm N của tam giác này nằm trên cạnh CO thỏa mãn CN = $\frac{2}{3}$ CO nên ON = $\frac{1}{3}$ CO.

Mà AO = CO.

Do đó: ON = OM.

Và O, M, N thẳng hàng (cùng thuộc đường chéo AC).

Nên O là trung điểm của MN.

Suy ra $\vec{O M} + \vec{O N} = \vec{0}$ .

Mà $\vec{P M} + \vec{P N} = \vec{0}$ nên điểm P trùng với điểm O.

Vậy điểm P thỏa mãn $\bar{P M} + \bar{P N} = \vec{0}$ là tâm O của hình bình hành ABCD.

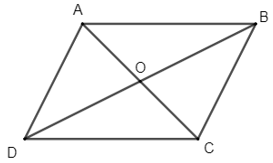
Bài 1 trang 93 Toán lớp 10 Tập 1: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo và một điểm M tùy ý. Chứng minh rằng:

a) $\vec{B A} + \vec{D C} = \vec{0}$ ;

b) $\vec{M A} + \vec{M C} = \vec{M B} + \vec{M D}$

Lời giải:

Cho hình bình hành ABCD có O là giao điểm của hai đường chéo và một điểm M

a) Do ABCD là hình bình hành nên $\vec{A B} = \vec{D C}$ .

Do đó: $\vec{B A} + \vec{D C} = \vec{B A} + \vec{A B} = \vec{B B} = \vec{0}$ .

Vậy $\vec{B A} + \vec{D C} = \vec{0}$ .

b) Vì O là giao điểm của hai đường chéo AC và BD của hình bình hành ABCD nên O là trung điểm của AC và BD.

Do đó: $\vec{O A} + \vec{O C} = \vec{0}; \vec{O B} + \vec{O D} = \vec{0}$ .

Ta có: $\vec{M A} + \vec{M C} = (\vec{M O} + \vec{O A}) + (\vec{M O} + \vec{O C})$

$= \vec{M O} + \vec{M O} + (\vec{O A} + \vec{O C}) = \vec{M O} + \vec{M O} + \vec{0} = \vec{M O} + \vec{M O}$ (1)

Và $\vec{M B} + \vec{M D} = (\vec{M O} + \vec{O B}) + (\vec{M O} + \vec{O D})$

$= \vec{M O} + \vec{M O} + (\vec{O B} + \vec{O D}) = \vec{M O} + \vec{M O} + \vec{0} = \vec{M O} + \vec{M O}$ (2)

Từ (1) và (2) suy ra $\vec{M A} + \vec{M C} = \vec{M B} + \vec{M D}$

Bài 2 trang 93 Toán lớp 10 Tập 1: Cho tứ giác ABCD, thực hiện các phép cộng và trừ vectơ sau:

a) $\vec{A B} + \vec{B C} + \vec{C D} + \vec{D A}$ ;

b) $\vec{A B} - \vec{A D}$ ;

c) $\vec{C B} - \vec{C D}$ .

Lời giải:

a) Ta có:

$\vec{A B} + \vec{B C} + \vec{C D} + \vec{D A}$

$= (\vec{A B} + \vec{B C}) + (\vec{C D} + \vec{D A})$

$= \vec{A C} + \vec{C A} = \vec{A A} = \vec{0}$

Vậy $\vec{A B} + \vec{B C} + \vec{C D} + \vec{D A} = \vec{0}$ .

b) Ta có: $\vec{A B} - \vec{A D} = \vec{D B}$ .

c) Ta có: $\vec{C B} - \vec{C D} = \vec{D B}$ .

Bài 3 trang 93 Toán lớp 10 Tập 1: Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ:

a) $\vec{B A} + \vec{A C}$ ;

b) $\vec{A B} + \vec{A C}$ ;

c) $\bar{B A} - \bar{B C}$ .

Lời giải:

a) Ta có: $\vec{B A} + \vec{A C} = \vec{B C}$

Do đó: $|\vec{B A} + \vec{A C}| = |\vec{B C}| = B C = a$ .

Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ: vectơ BC + vectơ AC

Dựng hình bình hành ABDC, nối A với D.

Áp dụng quy tắc hình hình hành ta có: $\vec{A B} + \vec{A C} = \vec{A D}$ .

Khi đó $|\vec{A B} + \vec{A C}| = |\vec{A D}| = A D$ .

Do tam giác ABC đều nên AB = AC = BC = a.

Suy ra hình bình hành ABDC là hình thoi.

Nên BD = AB = a.

Ta có: $\hat{C A B} = 60 °$ (tam giác ABC đều)

Suy ra $\hat{A B D} = 180 ° - \hat{C A B} = 180 ° - 60 ° = 120 °$ (AC // BD, hai góc trong cùng phía bù nhau).

Xét tam giác ABD, áp dụng định lí côsin ta có:

AD² = AB² + BD² – 2 . AB . BD . cosB

= a² + a² – 2 . a . a . cos120° = 3a²

Suy ra $A D = a \sqrt{3}$ .

Vậy $|\vec{A B} + \vec{A C}| = A D = a \sqrt{3}$ .

c) Ta có: $\vec{B A} - \vec{B C} = \vec{C A}$

Do đó: $|\vec{B A} - \vec{B C}| = |\vec{C A}| = C A = a$ .

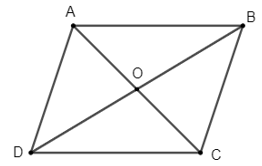
Bài 4 trang 93 Toán lớp 10 Tập 1: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Chứng minh rằng:

a) $\vec{O A} - \vec{O B} = \vec{O D} - \vec{O C}$ ;

b) $\vec{F_{2}}$ $\vec{O A} - \vec{O B} + \vec{D C} = \vec{0}$ .

Lời giải:

Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Chứng minh rằng: vectơ OA - vectơ OB = vectơ OD - vectơ OC

a) Ta có: $\vec{O A} - \vec{O B} = \vec{B A}$ ; $\vec{O D} - \vec{O C} = \vec{C D}$

ABCD là hình bình hành nên $\vec{B A} = \vec{C D}$

Vậy $\vec{O A} - \vec{O B} = \vec{O D} - \vec{O C}$ .

b) Ta có: $\vec{O A} - \vec{O B} + \vec{D C} = \vec{B A} + \vec{D C} = \vec{C D} + \vec{D C} = \vec{C C} = \vec{0}$ .

Vậy $\vec{O A} - \vec{O B} + \vec{D C} = \vec{0}$ .

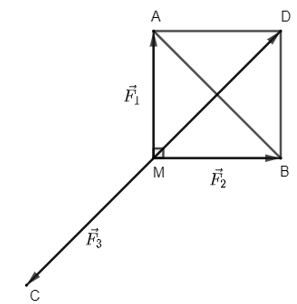
Bài 5 trang 93 Toán lớp 10 Tập 1: Cho ba lực $\vec{F_{1}} = \vec{M A}, \vec{F_{2}} = \vec{M B}$ và $\vec{F_{3}} = \vec{M C}$ cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của $\vec{F_{1}}, \vec{F_{2}}$ đều là 10 N và $\hat{A M B} = 90 °$ . Tìm độ lớn của lực $\vec{F_{3}}$ .

Lời giải:

Cho ba lực cùng tác động vào một vật tại điểm M và vật đứng yên

Vì ba lực $\vec{F_{1}}, \vec{F_{2}}, \vec{F_{3}}$ cùng tác động vào vật tại điểm M và vật đứng yên.

Do đó: $\vec{F_{1}} + \vec{F_{2}} + \vec{F_{3}} = \vec{0} \Leftrightarrow \vec{F_{3}} = - (\vec{F_{1}} + \vec{F_{2}})$ (1).

Ta cần tính $\vec{F_{1}} + \vec{F_{2}}$ .

Cường độ của $\vec{F_{1}}$ và $\vec{F_{2}}$ đều là 10 N.

$\Rightarrow |\vec{F_{1}}| = |\vec{F_{2}}| = 10 N .$

Dựng hình bình hành MADB có $\vec{F_{1}} = \vec{M A}, \vec{F_{2}} = \vec{M B}$ và $\hat{A M B} = 90 °$ .

Vì $|\vec{F_{1}}| = |\vec{F_{2}}| = 10 N$ nên MA = MB = 10.

Do đó MADB là hình vuông có cạnh bằng 10.

Suy ra đường chéo MD = $10 \sqrt{2}$ .

Do MADB là hình bình hà nh nên $\vec{M D} = \vec{M A} + \vec{M B}$ .

$\Rightarrow \vec{M D} = \vec{F_{1}} + \vec{F_{2}}$ (2).
Từ (1) và (2) suy ra: $\vec{F_{3}} = - (\vec{F_{1}} + \vec{F_{2}}) = - \vec{M D}$ .

Vậy lực $\vec{F_{3}}$ có hướng ngược với hướng của $\vec{M D}$ và có độ lớn: $|\vec{F_{3}}| = |\vec{M D}| = 10 \sqrt{2} N .$

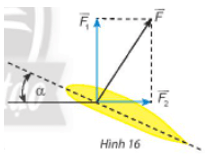
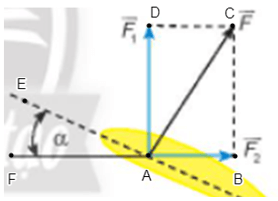
Bài 6 trang 93 Toán lớp 10 Tập 1: Khi máy bay nghiêng cánh một góc α, lực $\vec{F}$ của không khí tác động vuông góc với cánh và bằng tổng của lực nâng $\vec{F_{1}}$ và lực cản $\vec{F_{2}}$ (Hình 16). Cho biết α = 30° và $|\vec{F}| = a$ . Tính $|\vec{F_{1}}|$ và $|\vec{F_{2}}|$ theo a.

Khi máy bay nghiêng cánh một góc Alpha, lực F của không khí tác động vuông góc với cánh

Lời giải:

Đặt tên các điểm như hình vẽ dưới đây:

Khi máy bay nghiêng cánh một góc Alpha, lực F của không khí tác động vuông góc với cánh

Vì lực $\vec{F}$ của không khí tác động vuông góc với cánh nên góc tạo bởi lực $\vec{F}$ và cánh máy bay là $\vec{E A} C =$ 90°.

Ta có: $\hat{F A E} + \hat{E A C} + \hat{C A B} = 180 °$

$\Leftrightarrow α + 90 ° + \hat{C A B} = 180 °$

Suy ra: $\hat{C A B} = 180 ° - 90 ° - 30 ° = 60 °$

Tam giác ABC vuông tại B có AC = $|\vec{F}| = a$ , $\hat{C A B} = 60 °$ .

Khi đó: AB = AC . cos60° = $a . \frac{1}{2} = \frac{a}{2}$

BC = AC . sin60° = a . $\frac{\sqrt{3}}{2} = \frac{a \sqrt{3}}{2}$

Ta có: AD = BC = $\frac{a \sqrt{3}}{2}$ .

Vậy $|\vec{F_{1}}| = A D = \frac{a \sqrt{3}}{2}; |\vec{F_{2}}| = A B = \frac{a}{2}$

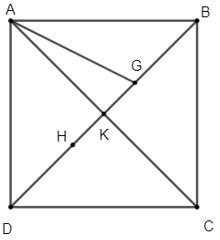
Bài 7 trang 93 Toán lớp 10 Tập 1: Cho hình vuông ABCD có cạnh bằng a và ba điểm G, H, K thỏa mãn: $\vec{K A} + \vec{K C} = \vec{0}; \vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ ; $\vec{H A} + \vec{H D} + \vec{H C} = \vec{0}$ . Tính độ dài các vectơ $\vec{K A}, \vec{G H}, \vec{A G}$ .

Lời giải:

Cho hình vuông ABCD có cạnh bằng a và ba điểm G, H, K thỏa mãn: vectơ KA + vectơ KC = vectơ 0

Vì K là điểm thỏa mãn $\vec{K A} + \vec{K C} = \vec{0}$ nên K là trung điểm của AC.

Vì G là điểm thỏa mãn $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ nên G là trọng tâm của tam giác ABC.

Vì H là điểm thỏa mãn $\vec{H A} + \vec{H D} + \vec{H C} = \vec{0}$ nên H là trọng tâm của tam giác ADC.

Do ABCD là hình vuông nên hai đường chéo AC, BD bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường nên K cũng là trung điểm của BD hay K chính là tâm của hình vuông ABCD.

Trong tam giác ABC, có BK là đường trung tuyến nên G ∈ BK và $G K = \frac{1}{3} B K$ (suy ra từ tính chất trọng tâm tam giác).

Trong tam giác ADC, có DK là đường trung tuyến nên H ∈ DK và $H K = \frac{1}{3} D K$ (suy ra từ tính chất trọng tâm tam giác).

Suy ra H, K, G thẳng hàng và cùng thuộc DB.

Hình vuông ABCD cạnh a nên AC = BD = $a \sqrt{2}$ .

Khi đó: AK = KC = DK = KB = $\frac{1}{2} A C = \frac{1}{2} B D = \frac{a \sqrt{2}}{2}$

Ta có: GH = GK + KH = $\frac{1}{3} B K + \frac{1}{3} D K = \frac{1}{3} . (\frac{a \sqrt{2}}{2} + \frac{a \sqrt{2}}{2}) = \frac{a \sqrt{2}}{3}$

Lại có: $G K = \frac{1}{3} B K = \frac{1}{3} . \frac{a \sqrt{2}}{2} = \frac{a \sqrt{2}}{6}$ .

Xét tam giác AKG vuông tại K (AC ⊥ BD tại K), áp dụng định lí Pythagore ta có:

AG² = AK² + KG² $= {(\frac{a \sqrt{2}}{2})}^{2} + {(\frac{a \sqrt{2}}{6})}^{2} = \frac{5 a}{9}$

Suy ra AG = $\frac{a \sqrt{5}}{3}$ .

Vậy ta tính được độ dài các vectơ $\vec{K A}, \vec{G H}, \vec{A G}$ là:

$\begin{array}{l} |\vec{K A}| = K A = \frac{a \sqrt{2}}{2} \\ |\vec{G H}| = G H = \frac{a \sqrt{2}}{3} \\ |\vec{A G}| = A G = \frac{a \sqrt{5}}{3} \end{array}$

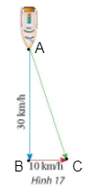
Bài 8 trang 93 Toán lớp 10 Tập 1: Một con tàu có vectơ vận tốc chỉ theo hướng nam, vận tốc của dòng nước là một vectơ theo hướng đông như Hình 17. Tính độ dài vectơ tổng của hai vectơ mói trên.

Một con tàu có vectơ vận tốc chỉ theo hướng nam, vận tốc của dòng nước

Lời giải:

Ta đặt tên các điểm như hình vẽ sau:

Một con tàu có vectơ vận tốc chỉ theo hướng nam, vận tốc của dòng nước

Khi đó vectơ vận tốc con tàu là $\vec{A B}$ với $|\vec{A B}| = A B = 30 k m / h$ .

Vectơ vận tốc dòng nước là $\vec{B C}$ với $|\vec{B C}| = B C = 10 k m / h$ .

Ta có vectơ tổng của hai vectơ trên là $\vec{A B} + \vec{B C} = \vec{A C}$

Do đó: $|\vec{A B} + \vec{B C}| = |\vec{A C}| = A C$

Lại có AB và BC vuông góc nên tam giác ABC vuông tại B, áp dụng định lí Pythagore ta có: AC² = AB² + BC² = 30² + 10² = 1000

Suy ra AC = $10 \sqrt{10}$ km/h.

Vậy độ dài của vectơ tổng của hai vectơ đã cho là $|\vec{A B} + \vec{B C}| = |\vec{A C}| = A C = 10 \sqrt{10}$ km/h.

Lời giải bài tập Toán lớp 10 Bài 2: Tổng và hiệu của hai vectơ Chân trời sáng tạo hay khác:

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯