Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d1: căn bậc hai 3x+y=0 và d2: căn bậc hai 3x-y=0 .

Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d₁: $\sqrt{3}x+y=0$ và d₂: $\sqrt{3}x-y=0$. Gọi (C) là đường tròn tiếp xúc với d₁ tại điểm A có hoành độ dương, (C) cắt d₂ tại hai điểm B, C sao cho tam giác ABC vuông tại B và có diện tích bằng $\frac{\sqrt{3}}{2}$. Phương trình của đường tròn (C) là:

Hướng dẫn giải

Đáp án đúng là: D

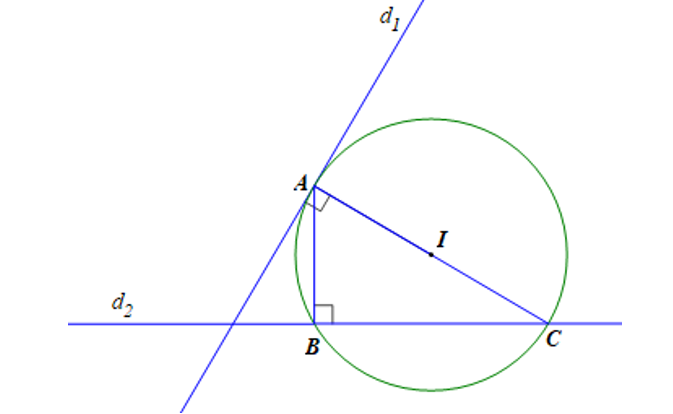
Vì A ∈ d₁ nên $A\left(a;-a\sqrt{3}\right)\left(a>0\right)$

    B, C ∈ d₂ nên $B\left(b;b\sqrt{3}\right),C\left(c;c\sqrt{3}\right)$.

Suy ra $\overrightarrow{AB}=\left(b-a;b\sqrt{3}+a\sqrt{3}\right),\overrightarrow{AC}=\left(c-a;c\sqrt{3}+a\sqrt{3}\right),\overrightarrow{BC}=\left(c-b;c\sqrt{3}-b\sqrt{3}\right)$

Đường thẳng d₁: $\sqrt{3}x+y=0$ có vectơ pháp tuyến là ${\overrightarrow{n}}_1=\left(\sqrt{3};1\right)$ nên có vectơ chỉ phương là ${\overrightarrow{u}}_1=\left(1;-\sqrt{3}\right)$.

Đường thẳng d₂: $\sqrt{3}x-y=0$ có vectơ pháp tuyến là ${\overrightarrow{n}}_2=\left(\sqrt{3};-1\right)$ nên có vectơ chỉ phương là ${\overrightarrow{u}}_2=\left(1;\sqrt{3}\right)$.

Ba điểm A, B, C đều nằm trên đường tròn mà tam giác ABC vuông tại B

Do đó AC là đường kính của đường tròn (C).

$\Rightarrow$ AC ⊥ d₁ $\iff \overrightarrow{AC}.{\overrightarrow{u}}_1=0\iff 1.\left(c-a\right)-\sqrt{3}\left(c\sqrt{3}+a\sqrt{3}\right)=0$

$\iff$ c – a – 3c – 3a = 0 Û 2a + c = 0     (1).

Lại có tam giác ABC vuông tại B nên AB ⊥ d₂

$\iff \overrightarrow{AB}.\overrightarrow{u_2}=0\iff 1. (b-a)+\sqrt{3}.(b\sqrt{3}+a\sqrt{3})=0$

$\iff$ b – a + 3b + 3a = 0 $\iff$ a + 2b = 0    (2).

Mặt khác $S_{ABC}=\frac{\sqrt{3}}{2}\iff \frac{1}{2}.d\left(A;d_2\right).BC=\frac{\sqrt{3}}{2}$

$\iff \frac{\left|\sqrt{3}.a-\left(-a\sqrt{3}\right)\right|}{\sqrt{{\left(\sqrt{3}\right)}^2+{\left(-1\right)}^2}}.\sqrt{{\left(c-b\right)}^2+{\left(c\sqrt{3}-b\sqrt{3}\right)}^2}=\sqrt{3}$

$\iff \frac{\left|2a\sqrt{3}\right|}{2}.\sqrt{4{\left(c-b\right)}^2}=\sqrt{3}\iff \frac{2a\sqrt{3}}{2}.2\left|c-b\right|=\sqrt{3}$ (do a > 0)

$\iff$ 2a|c – b| = 1      (3)

Từ (1) và (2) suy ra 2(2a + c) – (a + 2b) = 2 Û 2c – 2b = –3a

Thay vào (2) ta được a.|–3a| = 1 Û 3a² = 1 (do a > 0)

$\iff a=\frac{\sqrt{3}}{3}$(do a > 0).

Khi đó $b=-\frac{\sqrt{3}}{6},c=-\frac{2\sqrt{3}}{3}$

$\Rightarrow A\left(\frac{\sqrt{3}}{3};-1\right),C\left(-\frac{2\sqrt{3}}{3};-2\right)$ và $\overrightarrow{AC}=\left(-\sqrt{3};-1\right)$

Đường tròn (C) có AC là đường kính nên nhận trung điểm $I\left(-\frac{\sqrt{3}}{6};-\frac{3}{2}\right)$ của AC làm tâm và bán kính $R=\frac{AC}{2}=\frac{\sqrt{{\left(-\sqrt{3}\right)}^2+{\left(-1\right)}^2}}{2}=1$.

Vậy phương trình đường tròn cần tìm là $\left(C\right):{\left(x+\frac{\sqrt{3}}{6}\right)}^2+{\left(y+\frac{3}{2}\right)}^2=1.$