Vận dụng trang 37 Toán 10 Tập 1 Chân trời sáng tạo
Một người bán nước giải khát đang có 24 g bột cam, 9 nước và 210 g đường để pha chế hai loại nước cam A và B. Để pha chế 1 nước cam loại A cần 30 g đường, 1 nước và 1 g bột cam; để pha chế 1 nước cam loại B cần 10 g đường, 1 nước và 4 g bột cam. Mỗi lít nước cam loại A bán được 60 nghìn đồng, mỗi lít nước cam loại B bán được 80 nghìn đồng. Người đó nên pha chế bao nhiêu lít nước cam mỗi loại để có doanh thu cao nhất ?
Giải Toán lớp 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn
Vận dụng trang 37 Toán lớp 10 Tập 1: Một người bán nước giải khát đang có 24 g bột cam, 9 l nước và 210 g đường để pha chế hai loại nước cam A và B. Để pha chế 1 l nước cam loại A cần 30 g đường, 1 l nước và 1 g bột cam; để pha chế 1 l nước cam loại B cần 10 g đường, 1 l nước và 4 g bột cam. Mỗi lít nước cam loại A bán được 60 nghìn đồng, mỗi lít nước cam loại B bán được 80 nghìn đồng. Người đó nên pha chế bao nhiêu lít nước cam mỗi loại để có doanh thu cao nhất ?
Lời giải:
Gọi x là số lít nước cam loại A và y là số lít nước cam loại B có thể pha chế được.
- Hiển nhiên x ≥ 0 và y ≥ 0.
Để pha chế x lít nước cam loại A cần 30x gam đường, x lít nước và x gam bột cam.
Để pha chế y lít nước cam loại B cần 10y gam đường, y lít nước và 4y gam bột cam.
Tổng số đường cần dùng là: 30x + 10y (g); tổng số nước cần dùng là x + y (l) ; tổng số bột cam cần dùng là: x + 4y (gam).
- Do chỉ có 210 gam đường nên ta có bất phương trình: 30x + 10y ≤ 210, hay 3x + y ≤ 21.
- Do chỉ có 9 l nước nên ta có bất phương trình: x + y ≤ 9.
- Do chỉ có 24 gam bột cam nên ta có bất phương trình: x + 4y ≤ 24
Từ đó, ta có hệ bất phương trình mô tả các điều kiện ràng buộc đối với x và y là:
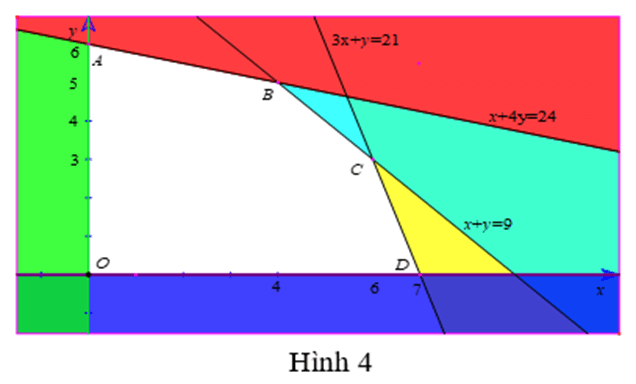
Biểu diễn miền nghiệm của hệ bất phương trình này trên hệ trục tọa độ Oxy, ta được hình 4.
Miền nghiệm của hệ bất phương trình là miền không tô màu (ngũ giác OABCD bao gồm cả các cạnh).
Tọa độ các đỉnh của ngũ giác đó là: O(0; 0); A (0; 6); B(4; 5); C(6; 3); D (7; 0).
Gọi F là doanh thu (đơn vị: nghìn đồng) của việc bán x lít nước cam loại A và y lít nước cam loại B.
Vì mỗi lít nước cam loại A bán được 60 nghìn đồng nên x lít nước cam loại A bán được 60x (nghìn đồng). Mỗi lít nước cam loại B bán được 80 nghìn đồng nên y lít nước cam loại B bán được 80y (nghìn đồng).
Tổng số tiền thu được là 60x + 80y (nghìn đồng)
Vì vậy, ta có: F(x ; y) = 60x + 80y.
Ta phải tìm x, y thỏa mãn hệ bất phương trình sao cho F đạt giá trị lớn nhất, nghĩa là tìm giá trị lớn nhất của biểu thức F = 60x + 80y trên miền ngũ giác OABCD.
Tính các giá trị của F tại các đỉnh của ngũ giác, ta có :
Tại O(0 ; 0) : F = 60.0 + 80.0 = 0 ;
Tại A(0 ; 6) : F = 60.0 + 80.6 = 480 ;
Tại B(4 ; 5) : F = 60.4 + 80.5 = 640 ;
Tại C(6 ; 3) : F = 60.6 + 80.3 = 600 ;
Tại D(7 ; 0) : F = 60.7 + 80.0 = 420 ;
F đạt giá trị lớn nhất bằng 640 tại B(4 ; 5).
Vậy để có doanh thu cao nhất thì người đó nên pha chế 4 lít nước cam loại A và 5 lít nước cam loại B.
Lời giải bài tập Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn hay, chi tiết khác: