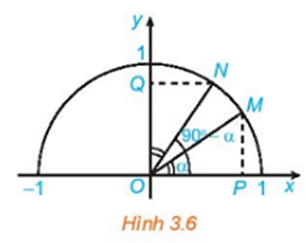
Trong Hình 3.6 hai điểm M, N ứng với hai góc phụ nhau alpha và 90 độ - alpha )góc xOM
Câu hỏi:
Trong Hình 3.6 hai điểm M, N ứng với hai góc phụ nhau và . Chứng minh rằng ΔMOP = ΔNOQ. Từ đó nêu mối quan hệ giữa và
Trả lời:
Ta có:
Dễ thấy: .
Xét ∆NOQ và ∆MOP có:
OM = ON = 1 (bán kính đường tròn đơn vị).
.
Do đó ΔNOQ = ΔMOP (cạnh huyền – góc nhọn)
Suy ra OP = OQ (hai cạnh tương ứng)
Ta có: OP = cos α, OQ = sin (90o – α).
Ta có: OP = , OQ =
.
Do đó: cos α = sin (90o − α).