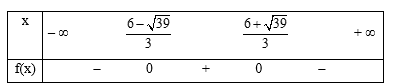Bài 6.16 trang 24 Toán 10 Tập 2 - Kết nối tri thức
Giải các bất phương trình bậc hai:
Giải Toán lớp 10 Bài 17: Dấu của tam thức bậc hai
Bài 6.16 trang 24 Toán 10 Tập 2: Giải các bất phương trình bậc hai:
a) x2 – 1 ≥ 0;
b) x2 – 2x – 1 < 0;
c) – 3x2 + 12x + 1 ≤ 0;
d) 5x2 + x + 1 ≥ 0.
Lời giải:
a) Tam thức f(x) = x2 – 1 có ∆ = 02 – 4 . 1 . (– 1) = 4 > 0 nên f(x) có hai nghiệm x1 = – 1 và x2 = 1.
Mặt khác hệ số a = 1 > 0, do đó ta có bảng xét dấu sau:
Tập nghiệm của bất phương trình là S = (– ∞; – 1] ∪ [1; + ∞).
b) Tam thức f(x) = x2 – 2x – 1 có ∆' = (– 1)2 – 1 . (– 1) = 2 > 0 nên f(x) có hai nghiệm x1 = 1 và x2 = 1 + .
Mặt khác hệ số a = 1 > 0, do đó ta có bảng xét dấu sau:
Vậy tập nghiệm của bất phương trình là S = .
c) Tam thức f(x) = – 3x2 + 12x + 1 có ∆' = 62 – (– 3) . 1 = 39 > 0 nên f(x) có hai nghiệm và .
Mặt khác hệ số a = – 3 < 0, do đó ta có bảng xét dấu sau:
Vậy tập nghiệm của bất phương trình là S = .
d) Tam thức f(x) = 5x2 + x + 1 có ∆ = 12 – 4 . 5 . 1 = – 19 < 0 và hệ số a = 5 > 0 nên f(x) luôn dương (cùng dấu a) với mọi .
Vậy tập nghiệm của bất phương trình là .
Lời giải bài tập Toán 10 Bài 17: Dấu của tam thức bậc hai hay, chi tiết khác:
HĐ1 trang 19 Toán 10 Tập 2: Hãy chỉ ra một vài đặc điểm chung của các biểu thức dưới đây ....
Luyện tập 1 trang 19 Toán 10 Tập 2: Hãy cho biết biểu thức nào sau đây là tam thức bậc hai ....
HĐ2 trang 19 Toán 10 Tập 2: Cho hàm số bậc hai y = f(x) = x2 – 4x + 3. ....
HĐ3 trang 20 Toán 10 Tập 2: Cho đồ thị hàm số y = g(x) = – 2x2 + x + 3 như Hình 6.18 ....
HĐ4 trang 20 Toán 10 Tập 2: Nêu nội dung thay vào ô có dấu “?” trong bảng sau cho thích hợp ....