Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:
Câu hỏi:
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:
a)
b) MA2 + MB2 – AB2 = 2MA.MB.cos và MA2 + MC2 – AC2 = 2MA.MC.cos;
c) (công thức đường trung tuyến).
Trả lời:
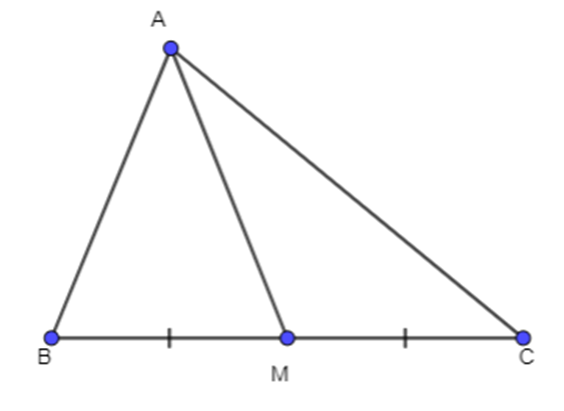
a)
Ta có:
b) Áp dụng định lí côsin trong ΔAMB, ta có:
AB2 = MA2 + MB2 – 2MA.MB.cos
⇔ MA2 + MB2 – AB2 = 2MA.MB.cos (1)
Áp dụng định lí côsin trong ΔAMC, ta có:
AC2 = MA2 + MC2 – 2MA.MC.cos
⇔ MA2 + MC2 – AC2 = 2MA.MC.cos (2)
c) Cộng vế với vế của (1) với (2), ta được:
MA2 + MB2 – AB2 + MA2 + MC2 – AC2
= 2MA.MB.cos + 2MA.MC.cos
(Vì )
2MA2 = AB2 + AC2 – – + 2MA.MB.cos + 2MA.MB.cos
Û 2MA2 = AB2 + AC2 – + 2MA.MB.(cos + cos )
Û 2MA2 = AB2 + AC2 –
Û
(công thức đường trung tuyến).