Chuyển động của một vật thể được thể hiện trên mặt phẳng Oxy. Vật thể khởi hành từ A(2; 1) và chuyển động thẳng đều với vectơ vận tốc \(\overrightarrow v \left( {3;4} \right)\). a) Hỏi vật t
Câu hỏi:
Chuyển động của một vật thể được thể hiện trên mặt phẳng Oxy. Vật thể khởi hành từ A(2; 1) và chuyển động thẳng đều với vectơ vận tốc \(\overrightarrow v \left( {3;4} \right)\).
a) Hỏi vật thể chuyển động trên đường thẳng nào (chỉ ra điểm đi qua và vectơ chỉ phương của đường thẳng đó)?
b) Chứng minh rằng, tại thời điểm t (t > 0) tính từ khi khởi hành, vật thể ở vị trí có tọa độ là (2 + 3t; 1 + 4t).
Trả lời:
Hướng dẫn giải
a) Vật thể chuyển động trên đường thẳng đi qua điểm A(2; 1) và nhận vectơ vận tốc \(\overrightarrow v \left( {3;4} \right)\) làm vectơ chỉ phương.
b) Gọi M(2 + 3t; 1 + 4t).
Có: \(\overrightarrow {AM} = \left( {2 + 3t - 2;1 + 4t - 1} \right) = \left( {3t;4t} \right) = t\left( {3;4} \right) = t\overrightarrow v \).
Do đó vectơ \(\overrightarrow {AM} \) và vectơ \(\overrightarrow v \) là hai vectơ cùng phương hay AM song song hoặc trùng với giá của \(\overrightarrow v \).
Khi đó điểm M thuộc đường thẳng chuyển động của vật thể, tức là đường thẳng đi qua điểm A và nhận vectơ vận tốc \(\overrightarrow v \) làm vectơ chỉ phương.
Vậy tại thời điểm t (t > 0) tính từ khi khởi hành, vật thể ở vị trí có tọa độ là (2 + 3t; 1 + 4t).
Xem thêm lời giải bài tập Toán 10 Kết nối tri thức hay, chi tiết:
Câu 1:
A. Các câu hỏi trong bài
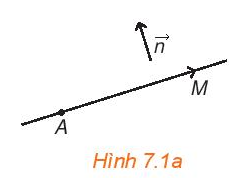
Cho vectơ và điểm A. Tìm tập hợp những điểm M sao cho \(\overrightarrow {AM} \) vuông góc với \(\overrightarrow n \).
Xem lời giải »
Câu 2:
Trong mặt phẳng tọa độ, cho đường thẳng ∆ đi qua điểm A(x0; y0) và có vectơ pháp tuyến \(\overrightarrow n \left( {a;b} \right)\). Chứng minh rằng điểm M(x; y) thuộc ∆ khi và chỉ khi
a(x – x0) + b(y – y0) = 0. (1) Xem lời giải »
Câu 3:
Trong mặt phẳng tọa độ, cho tam giác có ba đỉnh A(– 1; 5), B(2; 3), C(6; 1). Lập phương trình tổng quát của đường cao kẻ từ A của tam giác ABC.
Xem lời giải »
Câu 4:
Hãy chỉ ra một vectơ pháp tuyến của đường thẳng ∆: y = 3x + 4.
Xem lời giải »
Câu 5:
Lập phương trình tham số của đường thẳng ∆ đi qua hai điểm M(– 1; 2) và song song với đường thẳng d: 3x – 4y – 1 = 0.
Xem lời giải »
Câu 6:
Lập phương trình tham số và phương trình tổng quát của đường thẳng đi qua hai điểm phân biệt A(x1; y1), B(x2; y2) cho trước.
Xem lời giải »
Câu 7:
Việc quy đổi nhiệt độ giữa đơn vị độ C (Anders Celsius, 1701 – 1744) và đơn vị độ F (Daniel Fahrenheit, 1686 – 1736) được xác định bởi hai mốc sau:
Nước đóng băng ở 0 °C, 32 °F;
Nước sôi ở 100 °C, 212 °F.
Trong quy đổi đó, nếu a °C tương ứng với b °F thì trên mặt phẳng tọa độ Oxy, điểm M(a; b) thuộc đường thẳng đi qua A(0; 32) và B(100; 212).
Hỏi 0 °F, 100 °F tương ứng với bao nhiêu độ C?

Xem lời giải »
Câu 8:
B. Bài tập
Trong mặt phẳng tọa độ, cho \(\overrightarrow n = \left( {2;\,1} \right),\,\overrightarrow v = \left( {3;\,2} \right),\,A\left( {1;\,3} \right),\,B\left( { - 2;\,1} \right)\).
a) Lập phương trình tổng quát của đường thẳng ∆1 đi qua A và có vectơ pháp tuyến \(\overrightarrow n \).
b) Lập phương trình tham số của đường thẳng ∆2 đi qua B và có vectơ chỉ phương \(\overrightarrow v \).
c) Lập phương trình tham số của đường thẳng AB.
Xem lời giải »


