Trong mặt phẳng tọa độ, cho vecto n = (2;1), vecto v =(3;2),A(1;3),\,B( - 2;1). a) Lập phương trình tổng quát của đường thẳng ∆1 đi qua A và có vectơ pháp tuyến
Câu hỏi:
B. Bài tập
Trong mặt phẳng tọa độ, cho \(\overrightarrow n = \left( {2;\,1} \right),\,\overrightarrow v = \left( {3;\,2} \right),\,A\left( {1;\,3} \right),\,B\left( { - 2;\,1} \right)\).
a) Lập phương trình tổng quát của đường thẳng ∆1 đi qua A và có vectơ pháp tuyến \(\overrightarrow n \).
b) Lập phương trình tham số của đường thẳng ∆2 đi qua B và có vectơ chỉ phương \(\overrightarrow v \).
c) Lập phương trình tham số của đường thẳng AB.
Trả lời:
Hướng dẫn giải
a) Đường thẳng ∆1 đi qua A(1; 3) và có vectơ pháp tuyến \(\overrightarrow n = \left( {2;1} \right)\), do đó phương trình tổng quát của ∆1 là: 2(x – 1) + 1(y – 3) = 0 hay 2x + y – 5 = 0.
b) Đường thẳng ∆2 đi qua B(– 2; 1) và có vectơ chỉ phương \(\overrightarrow v = \left( {3;\,\,2} \right)\), do đó phương trình tham số của ∆2 là \(\left\{ \begin{array}{l}x = - 2 + 3t\\y = 1 + 2t\end{array} \right.\).
c) Đường thẳng AB đi qua điểm A(1; 3) và nhận \(\overrightarrow {AB} = \left( { - 2 - 1;1 - 3} \right) = \left( { - 3; - 2} \right)\) làm vectơ chỉ phương nên phương trình tham số của đường thẳng AB là \(\left\{ \begin{array}{l}x = 1 - 3t\\y = 3 - 2t\end{array} \right.\).
Xem thêm lời giải bài tập Toán 10 Kết nối tri thức hay, chi tiết:
Câu 1:
A. Các câu hỏi trong bài
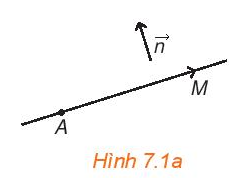
Cho vectơ và điểm A. Tìm tập hợp những điểm M sao cho \(\overrightarrow {AM} \) vuông góc với \(\overrightarrow n \).
Xem lời giải »
Câu 2:
Trong mặt phẳng tọa độ, cho đường thẳng ∆ đi qua điểm A(x0; y0) và có vectơ pháp tuyến \(\overrightarrow n \left( {a;b} \right)\). Chứng minh rằng điểm M(x; y) thuộc ∆ khi và chỉ khi
a(x – x0) + b(y – y0) = 0. (1) Xem lời giải »
Câu 3:
Trong mặt phẳng tọa độ, cho tam giác có ba đỉnh A(– 1; 5), B(2; 3), C(6; 1). Lập phương trình tổng quát của đường cao kẻ từ A của tam giác ABC.
Xem lời giải »
Câu 4:
Hãy chỉ ra một vectơ pháp tuyến của đường thẳng ∆: y = 3x + 4.
Xem lời giải »
Câu 5:
Lập phương trình đường thẳng tổng quát của các trục tọa độ.
Xem lời giải »
Câu 6:
Cho hai đường thẳng ∆1: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 + 5t\end{array} \right.\) và ∆2: 2x + 3y – 5 = 0.
a) Lập phương trình tổng quát của ∆1.
b) lập phương trình tham số của ∆2.
Xem lời giải »
Câu 7:
Trong mặt phẳng tọa độ, cho tam giác ABC có A(1; 2), B(3; 0) và C(– 2; – 1).
a) Lập phương trình đường cao kẻ từ A.
b) Lập phương trình đường trung tuyến kẻ từ B.
Xem lời giải »
Câu 8:
(Phương trình đoạn chắn của đường thẳng)
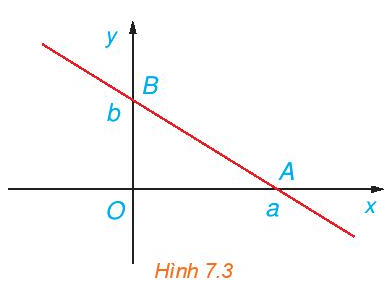
Chứng minh rằng, đường thẳng đi qua hai điểm A(a; 0), B(0; b) với ab ≠ 0 (H.7.3) có phương trình là \(\frac{x}{a} + \frac{y}{b} = 1\).
Xem lời giải »


