Khi nào tích vô hướng của hai vecto là một số dương? Là một số âm?

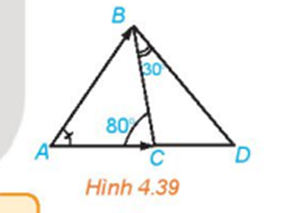
Trong Hình 4.39, số đo góc BAC cũng được gọi là số đo góc giữa hai vecto $\overrightarrow{AB}$ và $\overrightarrow{AC}$. Hãy tìm số đo các góc giữa $\overrightarrow{BC}$ và $\overrightarrow{BD}$, $\overrightarrow{DA}$ và $\overrightarrow{DB}$.

Khi nào thì góc giữa hai vecto bằng 0⁰, bằng 180⁰.

Cho tam giác ABC có BC = a, CA = b, AB = c. Hãy tính $\overrightarrow{AB}.\overrightarrow{AC}$ theo a, b, c.

Cho hai vecto cùng phương $\overrightarrow{u}=\left(x;y\right)$ và $\overrightarrow{v}=\left(kx;ky\right).$ Hãy kiểm tra công thức $\overrightarrow{u}.\overrightarrow{v}=k\left(x^2+y^2\right)$ theo từng trường hợp sau:

a) $\overrightarrow{u}=\overrightarrow{0};$

b) $\overrightarrow{u}\ne \overrightarrow{0}$ và $k\ge 0;$

c) $\overrightarrow{u}\ne \overrightarrow{0}$ và k < 0.

Trong mặt phẳng tọa độ Oxy, cho hai vecto không cùng phương $\overrightarrow{u}\left(x;y\right)$ và $\overrightarrow{v}\left(x\text{'};y\text{'}\right)$.

a) Xác định tọa độ các điểm A và B sao cho $\overrightarrow{OA}=\overrightarrow{u},\overrightarrow{OB}=\overrightarrow{v}.$

b) Tính AB², OA², OB² theo tọa độ của A và B.

c) Tính $\overrightarrow{OA}.\overrightarrow{OB}$ theo tọa độ của A, B.