Cho hai vecto cùng phương vecto u = (x; y) và vecto v = (kx; ky)

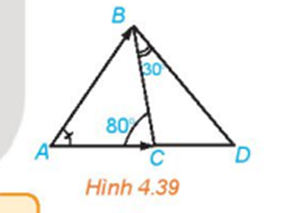
Trong Hình 4.39, số đo góc BAC cũng được gọi là số đo góc giữa hai vecto $\overrightarrow{AB}$ và $\overrightarrow{AC}$. Hãy tìm số đo các góc giữa $\overrightarrow{BC}$ và $\overrightarrow{BD}$, $\overrightarrow{DA}$ và $\overrightarrow{DB}$.

Khi nào thì góc giữa hai vecto bằng 0⁰, bằng 180⁰.

Khi nào tích vô hướng của hai vecto khác vectơ không $\overrightarrow{u},\overrightarrow{v}$ là một số dương? Là một số âm?

Trong mặt phẳng tọa độ Oxy, cho hai vecto không cùng phương $\overrightarrow{u}\left(x;y\right)$ và $\overrightarrow{v}\left(x\text{'};y\text{'}\right)$.

a) Xác định tọa độ các điểm A và B sao cho $\overrightarrow{OA}=\overrightarrow{u},\overrightarrow{OB}=\overrightarrow{v}.$

b) Tính AB², OA², OB² theo tọa độ của A và B.

c) Tính $\overrightarrow{OA}.\overrightarrow{OB}$ theo tọa độ của A, B.

Tính tích vô hướng và góc giữa hai vecto $\overrightarrow{u}\left(0;-5\right),\overrightarrow{v}\left(\sqrt{3};1\right)$.

Cho ba vecto $\overrightarrow{u}\left(x_1;y_1\right),\overrightarrow{v}\left(x_2;y_2\right),\overrightarrow{w}\left(x_3;y_3\right).$ 

a) Tính $\overrightarrow{u.}\left(\overrightarrow{v}+\overrightarrow{\text{w}}\right),\overrightarrow{u}.\overrightarrow{v}+\overrightarrow{u}.\overrightarrow{\text{w}}$ theo tọa độ các vecto $\overrightarrow{u},\overrightarrow{v},\overrightarrow{\text{w}}.$

b) So sánh $\overrightarrow{u}.\left(\overrightarrow{v}+\overrightarrow{\text{w}}\right)$ và $\overrightarrow{u}.\overrightarrow{v}+\overrightarrow{u}.\overrightarrow{\text{w}}$.

c) So sánh $\overrightarrow{u}.\overrightarrow{v}$ và $\overrightarrow{v}.\overrightarrow{u}$.

Cho tam giác ABC với A(-1;2), B(8;-1), C(8;8). Gọi H là trực tâm của tam giác ABC.

a) Chứng minh rằng $\overrightarrow{AH}.\overrightarrow{BC}=\overrightarrow{0}$ và $\overrightarrow{BH}.\overrightarrow{CA}=\overrightarrow{0}.$

b) Tìm tọa độ của H.

c) Giải tam giác ABC.