Cho tam giác ABC có BC = a, CA = b, AB = c. Hãy tính vecto AB. vecto AC theo a, b, c
Câu hỏi:
Cho tam giác ABC có BC = a, CA = b, AB = c. Hãy tính theo a, b, c.
Trả lời:
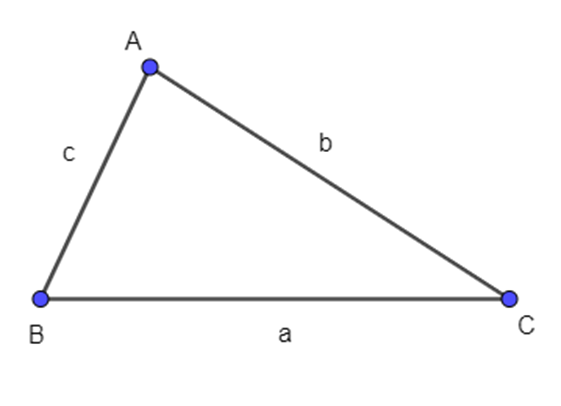
Ta có:
Theo định lí côsin, ta có:
.
Vậy
Câu hỏi:
Cho tam giác ABC có BC = a, CA = b, AB = c. Hãy tính theo a, b, c.
Trả lời:

Ta có:
Theo định lí côsin, ta có:
.
Vậy
Câu 1:
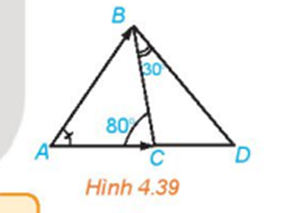
Trong Hình 4.39, số đo góc BAC cũng được gọi là số đo góc giữa hai vecto và . Hãy tìm số đo các góc giữa và , và .
Câu 4:
Khi nào tích vô hướng của hai vecto khác vectơ không là một số dương? Là một số âm?
Câu 5:
Cho hai vecto cùng phương và Hãy kiểm tra công thức theo từng trường hợp sau:
a)
b) và
c) và k < 0.
Câu 6:
Trong mặt phẳng tọa độ Oxy, cho hai vecto không cùng phương và .
a) Xác định tọa độ các điểm A và B sao cho
b) Tính AB2, OA2, OB2 theo tọa độ của A và B.
c) Tính theo tọa độ của A, B.
