Giải Toán 10 trang 38 Tập 2 Kết nối tri thức

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 38 Tập 2 trong Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách Toán lớp 10 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 38.

Giải Toán 10 trang 38 Tập 2 Kết nối tri thức

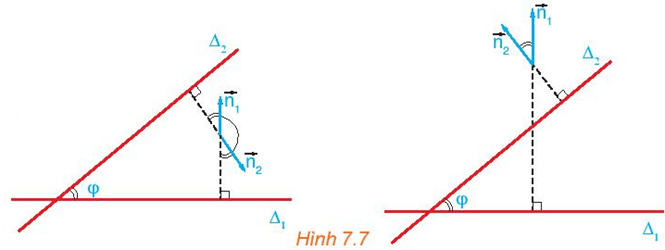
HĐ3 trang 38 Toán 10 Tập 2: Cho hai đường thẳng cắt nhau ∆₁, ∆₂ tương ứng có các vectơ pháp tuyến ${\overrightarrow{n}}_1,{\overrightarrow{n}}_2$. Gọi φ là góc giữa hai đường thẳng đó (H.7.7). Nêu mối quan hệ giữa: 

a) góc φ và góc $({\overrightarrow{n}}_1,{\overrightarrow{n}}_2\text{)}$;

b) cosφ và cos$({\overrightarrow{n}}_1,{\overrightarrow{n}}_2\text{)}$.

Lời giải:

a) Quan sát Hình 7.7, ta thấy góc giữa hai đường thẳng ∆₁ và ∆₂ là góc φ, góc này bằng hoặc bù với góc giữa hai vectơ ${\overrightarrow{n}}_1$ và ${\overrightarrow{n}}_2$. 

b) 

+) Với trường hợp góc φ và góc$({\overrightarrow{n}}_1,{\overrightarrow{n}}_2\text{)}$ bằng nhau thì ta có: cosφ = cos$({\overrightarrow{n}}_1,{\overrightarrow{n}}_2\text{)}$;

+) Với trường hợp góc φ và góc$({\overrightarrow{n}}_1,{\overrightarrow{n}}_2\text{)}$ bù nhau thì ta có: cosφ = – cos$({\overrightarrow{n}}_1,{\overrightarrow{n}}_2\text{)}$.

Luyện tập 2 trang 38 Toán 10 Tập 2: Tính góc giữa hai đường thẳng 

∆₁: x + 3y + 2 = 0 và ∆₂: y = 3x + 1. 

Lời giải:

Vectơ pháp tuyến của đường thẳng ∆₁ là ${\overrightarrow{n}}_1=\left(1;3\right)$.

Ta có: y = 3x + 1 ⇔ 3x – y + 1 = 0 hay ∆₂: 3x – y + 1 = 0, do đó vectơ pháp tuyến của đường thẳng ∆₂ là ${\overrightarrow{n}}_2=\left(3;-1\right)$. 

Gọi φ là góc giữa hai đường thẳng ∆₁ và ∆₂. Ta có: 

cosφ = $\left|\cos \left({\overrightarrow{n}}_1,{\overrightarrow{n}}_2\right)\right|=\frac{\left|{\overrightarrow{n}}_1.{\overrightarrow{n}}_2\right|}{\left|{\overrightarrow{n}}_1\right|.\left|{\overrightarrow{n}}_2\right|}=\frac{\left|1.3+3.\left(-1\right)\right|}{\sqrt{1^2+3^2}.\sqrt{3^2+{\left(-1\right)}^2}}=0$. 

Do đó hai đường thẳng ∆₁ và ∆₂ vuông góc và φ = 90°. 

Lời giải bài tập Toán lớp 10 Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách Kết nối tri thức hay khác:

• Giải Toán 10 trang 36

• Giải Toán 10 trang 37

• Giải Toán 10 trang 39

• Giải Toán 10 trang 40

• Giải Toán 10 trang 41