Giải Toán 10 trang 40 Tập 2 Kết nối tri thức

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 40 Tập 2 trong Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách Toán lớp 10 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 40.

Giải Toán 10 trang 40 Tập 2 Kết nối tri thức

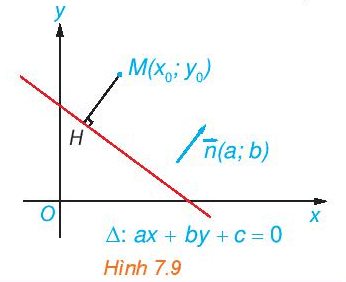
HĐ4 trang 40 Toán 10 Tập 2: Cho điểm M(x₀; y₀) và đường thẳng ∆: ax + by + c = 0 có vectơ pháp tuyến $\overrightarrow{n}\left(a;b\right)$. Gọi H là hình chiếu vuông góc của M trên ∆ (H.7.9). 

a) Chứng minh rằng $\left|\overrightarrow{n}.\overrightarrow{HM}\right|=\sqrt{a^2+b^2}.HM$.

b) Giả sử H có tọa độ (x₁; y₁). Chứng minh rằng: $\overrightarrow{n}.\overrightarrow{HM}$= a(x₀ – x₁) + b(y₀ – y₁) = ax₀ + by₀ + c. 

c) Chứng minh rằng $HM=\frac{\left|a{x}_0+b{y}_0+c\right|}{\sqrt{a^2+b^2}}$. 

Lời giải:

a) Do H là hình chiếu của M lên ∆ nên MH ⊥ ∆.

Vectơ $\overrightarrow{n}$ là vectơ pháp tuyến của ∆ nên giá của vectơ $\overrightarrow{n}$ vuông góc với ∆. 

Khi đó đường thẳng MH song song hoặc trùng với giá của vectơ $\overrightarrow{n}$ nên hai vectơ $\overrightarrow{HM}$ và $\overrightarrow{n}$cùng phương. 

Do đó hai vectơ $\overrightarrow{HM}$ và $\overrightarrow{n}$ cùng hướng hoặc ngược hướng.

+) Nếu hai vectơ $\overrightarrow{HM}$ và $\overrightarrow{n}$ cùng hướng thì $\overrightarrow{n}.\overrightarrow{HM}=\left|\overrightarrow{n}\right|.\left|\overrightarrow{HM}\right|=\sqrt{a^2+b^2}.HM$.

+) Nếu hai vectơ $\overrightarrow{HM}$ và $\overrightarrow{n}$ ngược hướng thì $\overrightarrow{n}.\overrightarrow{HM}=-\left|\overrightarrow{n}\right|.\left|\overrightarrow{HM}\right|=-\sqrt{a^2+b^2}.HM$.

Vậy $\left|\overrightarrow{n}.\overrightarrow{HM}\right|=\sqrt{a^2+b^2}.HM$. 

b) Vì H thuộc ∆ nên tọa độ của H thỏa mãn phương trình ∆, thay tọa độ của H vào phương trình ∆ ta được: ax₁ + by₁ + c = 0 ⇔ c = – ax₁ – by₁           (1). 

Ta lại có: $\overrightarrow{HM}=\left(x_0-x_1;y_0-y_1\right)$.

Suy ra: $\overrightarrow{n}.\overrightarrow{HM}=a\left(x_0-x_1\right)+b\left(y_0-y_1\right)$ = ax₀ + by₀ – ax₁ – by₁             (2). 

Từ (1) và (2) suy ra : $\overrightarrow{n}.\overrightarrow{HM}=a\left(x_0-x_1\right)+b\left(y_0-y_1\right)$ = ax₀ + by₀ + c. 

c) Theo câu a) ta có: $\left|\overrightarrow{n}.\overrightarrow{HM}\right|=\sqrt{a^2+b^2}.HM$. 

Theo câu b) ta có: $\overrightarrow{n}.\overrightarrow{HM}$ = ax₀ + by₀ + c. 

Suy ra: |ax₀ + by₀ + c| = $\sqrt{a^2+b^2}.HM$.

Vậy $HM=\frac{\left|a{x}_0+b{y}_0+c\right|}{\sqrt{a^2+b^2}}$.

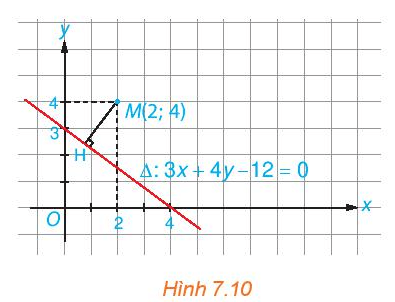
Trải nghiệm trang 40 Toán 10 Tập 2: Đo trực tiếp khoảng cách từ điểm M đến đường thẳng ∆ (H.7.10) và giải thích vì sao kết quả đo đạc đó phù hợp với kết quả tính toán trong lời giải Ví dụ 4. 

Lời giải:

Khoảng cách từ M đến đường thẳng ∆ là độ dài đoạn MH. 

Dùng thước ta đo được MH có độ dài bằng 2 ô vuông trên mặt phẳng tọa độ Oxy nên MH = 2. 

Kết quả này hoàn toàn phù hợp với kết quả tính được trong lời giải của Ví dụ 4 vì điểm M ở đây có tọa độ trùng với điểm M của Ví dụ 4 và đường thẳng Δ có phương trình trùng với phương trình trong Ví dụ 4.

Luyện tập 5 trang 40 Toán 10 Tập 2: Tính khoảng cách từ điểm M(1; 2) đến đường thẳng $\Delta :\left\{\begin{array}{l}x=5+3t\\ y=-5-4t\end{array}\right.$. 

Lời giải:

Đường thẳng $\Delta :\left\{\begin{array}{l}x=5+3t\\ y=-5-4t\end{array}\right.$đi qua điểm A(5; – 5) và có một vectơ chỉ phương là $\overrightarrow{u}=\left(3;-4\right)$, suy ra ∆ có vectơ pháp tuyến là $\overrightarrow{n}=\left(4;3\right)$. 

Do đó, phương trình tổng quát của ∆ là: 4(x – 5) + 3(y + 5) = 0 hay 4x + 3y – 5 = 0. 

Áp dụng công thức tính khoảng cách từ điểm M đến đường thẳng ∆, ta có: 

d(M, ∆) = $\frac{\left|4.1+3.2-5\right|}{\sqrt{4^2+3^2}}=\frac{5}{5}=1$. 

Vậy khoảng cách từ điểm M đến đường thẳng ∆ là 1. 

Lời giải bài tập Toán lớp 10 Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách Kết nối tri thức hay khác:

• Giải Toán 10 trang 36

• Giải Toán 10 trang 37

• Giải Toán 10 trang 38

• Giải Toán 10 trang 39

• Giải Toán 10 trang 41