Giải Toán 10 trang 61 Tập 1 Kết nối tri thức

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 61 Tập 1 trong Bài 10: Vectơ trong mặt phẳng tọa độ Toán lớp 10 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 61.

Giải Toán 10 trang 61 Tập 1 Kết nối tri thức

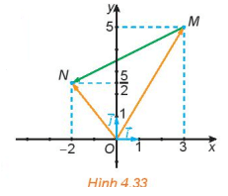
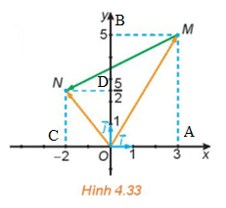
HĐ2 trang 61 Toán 10 Tập 1: Trong Hình 4.33:

a) Hãy biểu thị mỗi vecto $\overrightarrow{OM},\overrightarrow{ON}$ theo các vecto $\overrightarrow{i},\overrightarrow{j}$.

b) Hãy biểu thị vecto $\overrightarrow{MN}$ theo các vecto $\overrightarrow{OM},\overrightarrow{ON}$ từ đó biểu thị vecto $\overrightarrow{MN}$ theo các vecto $\overrightarrow{i},\overrightarrow{j}$.

Lời giải:

a) Xét hình bình hành OAMB, có:

$\overrightarrow{OM}=\overrightarrow{OA}+\overrightarrow{OB}=3\overrightarrow{i}+5\overrightarrow{j}$ (quy tắc hình bình hành)

Xét hình bình hành OCND, có:

$\overrightarrow{ON}=\overrightarrow{OC}+\overrightarrow{OD}=-2\overrightarrow{i}+\frac{5}{2}\overrightarrow{j}$ (quy tắc hình bình hành)

b) Xét tam giác OMN, có:

$\overrightarrow{MN}=\overrightarrow{ON}-\overrightarrow{OM}$ (quy tắc ba điểm)

$$\begin{gathered} \overrightarrow{MN}=\overrightarrow{ON}-\overrightarrow{OM} \\ =-2\overrightarrow{i}+\frac{5}{2}\overrightarrow{j}-\left(3\overrightarrow{i}+5\overrightarrow{j}\right)=-5\overrightarrow{i}-\frac{5}{2}\overrightarrow{j}. \end{gathered}$$

Luyện tập 1 trang 61 Toán 10 Tập 1: Tìm tọa độ của $\overrightarrow{0}$.

Lời giải:

Ta có: $\overrightarrow{0}=0.\overrightarrow{i}+0.\overrightarrow{j}\Rightarrow \overrightarrow{0}\left(0;0\right)$.

Vậy tọa độ của $\overrightarrow{0}$ là $\overrightarrow{0}\left(0;0\right).$

HĐ3 trang 61 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho $\overrightarrow{u}=\left(2;-3\right),\overrightarrow{v}=\left(4;1\right),\overrightarrow{a}=\left(8;-12\right).$

a) Hãy biểu thị mỗi vecto $\overrightarrow{u},\overrightarrow{v},\overrightarrow{a}$ theo các vecto $\overrightarrow{i},\overrightarrow{j}.$

b) Tìm tọa độ của các vecto $\overrightarrow{u}+\overrightarrow{v},4\overrightarrow{u}.$

c) Tìm mối liên hệ giữa hai vecto $\overrightarrow{u},\overrightarrow{a}.$

Lời giải:

a) Ta có:

$\overrightarrow{u}=\left(2;-3\right)\Rightarrow \overrightarrow{u}=2\overrightarrow{i}-3\overrightarrow{j};$

$\overrightarrow{v}=\left(4;1\right)\Rightarrow \overrightarrow{v}=4\overrightarrow{i}+\overrightarrow{j};$

$\overrightarrow{a}=\left(8;-12\right)\Rightarrow \overrightarrow{a}=8\overrightarrow{i}-12\overrightarrow{j}.$

b) Ta có:

$\overrightarrow{u}+\overrightarrow{v}=2\overrightarrow{i}-3\overrightarrow{j}+4\overrightarrow{i}+\overrightarrow{j}=6\overrightarrow{i}-2\overrightarrow{j}$

$\Rightarrow \overrightarrow{u}+\overrightarrow{v}=\left(6;-2\right)$

$4\overrightarrow{u}=4\left(2\overrightarrow{i}-3\overrightarrow{j}\right)=8\overrightarrow{i}-12\overrightarrow{j}$

$\Rightarrow 4\overrightarrow{u}=\left(8;-12\right).$

c) Ta có $\overrightarrow{a}=\left(8;-12\right)=4\overrightarrow{u}$.

Lời giải bài tập Toán lớp 10 Bài 10: Vectơ trong mặt phẳng tọa độ Kết nối tri thức hay khác:

• Giải Toán 10 trang 60
• Giải Toán 10 trang 62
• Giải Toán 10 trang 63
• Giải Toán 10 trang 64
• Giải Toán 10 trang 65