Giải Toán 10 trang 62 Tập 1 Kết nối tri thức

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 62 Tập 1 trong Bài 10: Vectơ trong mặt phẳng tọa độ Toán lớp 10 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 62.

Giải Toán 10 trang 62 Tập 1 Kết nối tri thức

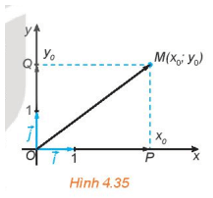
HĐ4 trang 62 Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy, cho điểm M(x₀;y₀) . Gọi P, Q tương ứng là hình chiếu vuông góc của M trên trục hoành Ox và trục tung Oy (H.4.35).

a) Trên trục Ox, điểm P biểu diễn số nào? Biểu thị $\overrightarrow{OP}$ theo $\overrightarrow{i}$ và tính độ dài của $\overrightarrow{OP}$ theo x₀.

b) Trên trục Oy, điểm Q biểu diễn số nào? Biểu thị $\overrightarrow{OQ}$ theo $\overrightarrow{j}$và tính độ dài của $\overrightarrow{OP}$ theo y₀.

c) Dựa vào hình chữ nhật OPMQ, tính độ dài của $\overrightarrow{OM}$ theo x₀, y₀.

d) Biểu thị $\overrightarrow{OM}$ theo các vecto $\overrightarrow{i},\overrightarrow{j}$.     

Lời giải:

a) Trên trục Ox, điểm P biểu diễn cho số x₀;

Độ dài đoạn thẳng OP = |x₀| = x₀.

Ta có vecto $\overrightarrow{OP}$ cùng hướng với vecto $\overrightarrow{i}$ và OP = x₀ nên $\overrightarrow{OP}=x_0\overrightarrow{i}.$

b) Trên trục Oy, điểm Q biểu diễn cho số y₀;

Độ dài đoạn thẳng OQ = |y₀| = y₀.

Ta có vecto $\overrightarrow{OQ}$ cùng hướng với vecto $\overrightarrow{j}$ và OQ = y₀ nên $\overrightarrow{OQ}=y_0\overrightarrow{j}.$

c) Xét tam giác OPM vuông tại P, có:

$OM=\sqrt{O{P}^2+M{P}^2}$

$=\sqrt{O{P}^2+O{Q}^2}=\sqrt{x_0^2+y_0^2}.$

Vậy $\left|\overrightarrow{OM}\right|=\sqrt{x_0^2+y_0^2}.$

d) Ta có

$\overrightarrow{OM}=\overrightarrow{OP}+\overrightarrow{OQ}=x_0\overrightarrow{i}+y_0\overrightarrow{j}$.

HĐ5 trang 62 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho các điểm M(x; y) và N(x’; y’).

a) Tìm tọa độ của các vecto $\overrightarrow{OM},\overrightarrow{ON}$.

b) Biểu thị vecto $\overrightarrow{MN}$ theo các vecto $\overrightarrow{OM},\overrightarrow{ON}$ và tìm tọa độ của $\overrightarrow{MN}.$

c) Tìm độ dài của vecto $\overrightarrow{MN}.$

Lời giải:

a) Ta có M(x; y) $\Rightarrow \overrightarrow{OM}\left(x;y\right)$

Ta lại có: N(x’; y’) $\Rightarrow \overrightarrow{ON}\left(x\text{'};y\text{'}\right)$

b) Ta có: $\overrightarrow{MN}=\overrightarrow{ON}-\overrightarrow{OM}$

Khi đó tọa độ của vecto $\overrightarrow{MN}$ là $\overrightarrow{MN}=\left(x\text{'}-x;y\text{'}-y\right).$

c) Độ dài của vecto $\overrightarrow{MN}$ là $\left|\overrightarrow{MN}\right|=\sqrt{{\left(x\text{'}-x\right)}^2+{\left(y\text{'}-y\right)}^2}.$

Lời giải bài tập Toán lớp 10 Bài 10: Vectơ trong mặt phẳng tọa độ Kết nối tri thức hay khác:

• Giải Toán 10 trang 60
• Giải Toán 10 trang 61
• Giải Toán 10 trang 63
• Giải Toán 10 trang 64
• Giải Toán 10 trang 65