Giải Toán 10 trang 67 Tập 1 Kết nối tri thức

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 67 Tập 1 trong Bài 11: Tích vô hướng của hai vectơ Toán lớp 10 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 67.

Giải Toán 10 trang 67 Tập 1 Kết nối tri thức

Câu hỏi trang 67 Toán 10 Tập 1: Khi nào tích vô hướng của hai vecto $\overrightarrow{u},\overrightarrow{v}$ là một số dương? Là một số âm?

Lời giải:

Tích vô hướng của hai vecto $\overrightarrow{u},\overrightarrow{v}\ne \overrightarrow{0}$ được tính bởi công thức sau:

$\overrightarrow{u}.\overrightarrow{v}=\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|.c\text{os}\left(\overrightarrow{u},\overrightarrow{v}\right).$

Vì $\left|\overrightarrow{u}\right|>0,\left|\overrightarrow{v}\right|>0$ nên dấu của $\overrightarrow{u}.\overrightarrow{v}$ phụ thuộc vào dấu của $c\text{os}\left(\overrightarrow{u},\overrightarrow{v}\right)$.

Nếu tích vô hướng của hai vecto $\overrightarrow{u},\overrightarrow{v}$ là một số dương thì $c\text{os}\left(\overrightarrow{u},\overrightarrow{v}\right)>0.$ Do đó góc giữa hai vecto $\overrightarrow{u},\overrightarrow{v}$ là góc nhọn hoặc bằng 0⁰.

Nếu tích vô hướng của hai vecto $\overrightarrow{u},\overrightarrow{v}$ là một số âm thì $c\text{os}\left(\overrightarrow{u},\overrightarrow{v}\right)<0.$ Do đó góc giữa hai vecto $\overrightarrow{u},\overrightarrow{v}$ là góc tù hoặc bằng 180⁰.

Câu hỏi trang 67 Toán 10 Tập 1: Khi nào thì ${\left(\overrightarrow{u}.\overrightarrow{v}\right)}^2={\overrightarrow{u}}^2.{\overrightarrow{v}}^2?$

Lời giải:

Ta có: $\overrightarrow{u}.\overrightarrow{v}=\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|.c\text{os}\left(\overrightarrow{u},\overrightarrow{v}\right)$

$\iff {\left(\overrightarrow{u}.\overrightarrow{v}\right)}^2={\left[\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|.c\text{os}\left(\overrightarrow{u},\overrightarrow{v}\right)\right]}^2$

$={\overrightarrow{u}}^2.{\overrightarrow{v}}^2.c{\text{os}}^2\left(\overrightarrow{u},\overrightarrow{v}\right)$

Để ${\left(\overrightarrow{u}.\overrightarrow{v}\right)}^2={\overrightarrow{u}}^2.{\overrightarrow{v}}^2$ thì $c{\text{os}}^2\left(\overrightarrow{u},\overrightarrow{v}\right)=1$

$\iff \left[\begin{array}{l}c\text{os}\left(\overrightarrow{u},\overrightarrow{v}\right)=1\\ c\text{os}\left(\overrightarrow{u},\overrightarrow{v}\right)=-1\end{array}\right.\iff \left[\begin{array}{l}\left(\overrightarrow{u},\overrightarrow{v}\right)=0^0\\ \left(\overrightarrow{u},\overrightarrow{v}\right)={180}^0\end{array}\right.$

Vậy khi góc giữa hai vecto $\overrightarrow{u},\overrightarrow{v}$ là 0⁰ hoặc 180⁰ thì ${\left(\overrightarrow{u}.\overrightarrow{v}\right)}^2={\overrightarrow{u}}^2.{\overrightarrow{v}}^2.$

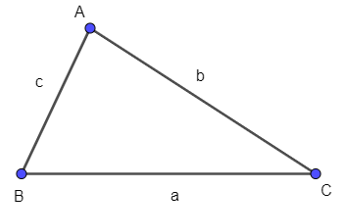
Luyện tập 2 trang 67 Toán 10 Tập 1: Cho tam giác ABC có BC = a, CA = b, AB = c. Hãy tính $\overrightarrow{AB}.\overrightarrow{AC}$ theo a, b, c.

Lời giải:

Ta có: $\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.c\text{os}\left(\overrightarrow{AB}.\overrightarrow{AC}\right)$

$=AB.AC.\cos BAC=bc.c\text{osBAC}$

Theo định lí cos, ta có:

$\text{cosBAC=}\frac{b^2+c^2-a^2}{2bc}$

$\overrightarrow{AB}.\overrightarrow{AC}=bc.\frac{b^2+c^2-a^2}{2bc}$

$=\frac{b^2+c^2-a^2}{2}$.

Vậy $\overrightarrow{AB}.\overrightarrow{AC}=\frac{b^2+c^2-a^2}{2}.$

Lời giải bài tập Toán lớp 10 Bài 11: Tích vô hướng của hai vectơ Kết nối tri thức hay khác:

• Giải Toán 10 trang 66
• Giải Toán 10 trang 68
• Giải Toán 10 trang 70