15 Bài tập Hàm số bậc hai (Trắc nghiệm Toán lớp 10 có đáp án) - Kết nối tri thức
Haylamdo biên soạn và sưu tầm với 15 bài tập trắc nghiệm Hàm số bậc hai Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
15 Bài tập Hàm số bậc hai (Trắc nghiệm Toán lớp 10 có đáp án) - Kết nối tri thức
Câu 1. Trục đối xứng của parabol y = x2 – 4x + 1
A. x = 2
B. x = – 2
C. x = 4
D. x = – 4
Câu 2. Tọa độ đỉnh I của hàm số y = – 3x2 + 4x – 1
A.
B.
C.
D.
Câu 3. Cho hàm số y = 2x2 – 4x – 1. Kết luận nào đúng trong các kết luận sau
A. Hàm số đồng biến trên khoảng (0; + ∞);
B. Hàm số đồng biến trên khoảng (– ∞; 1);
C. Hàm số nghịch biến trên khoảng (– ∞; 0);
D. Hàm số nghịch biến trên khoảng (– ∞; 2).
Câu 4. Cho parabol y = ax2 + bx – 3. Xác định hệ số a, b biết parabol có đỉnh
I(– 1; – 5)
A. a = 1; b = 2;
B. a = 1; b = – 2;
C. a = – 2; b = 4;
D. a = 2; b = 4.
Câu 5. Hàm số y = – x2 + 2x + 1 đồng biến trên khoảng
A. (– ∞; + ∞);
B. (– ∞; 1);
C. (1; + ∞);
D. (– ∞; 2).
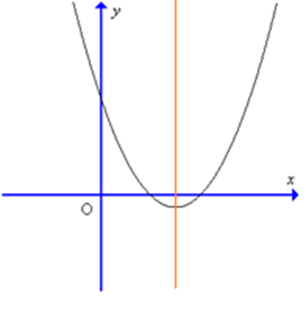
Câu 6. Cho parabol có đồ thị như hình sau:
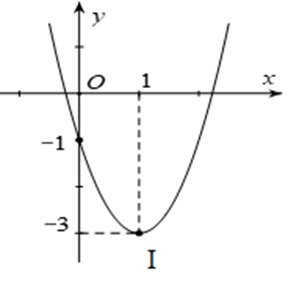
Tọa độ đỉnh I của parabol
A. I(– 1; – 3);
B. I(1; 0);
C. I(0; – 3);
D. I(1; – 3).
Câu 7. Cho hàm số y = f(x) có đồ thị như hình sau:
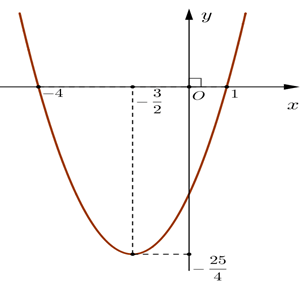
Hàm số đồng biến trên khoảng
A.
B.
C.
D.
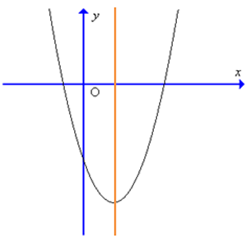
Câu 8. Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:
Kết luận nào sau đây đúng về hệ số a, b:
A. a > 0; b > 0;
B. a < 0; b > 0;
C. a > 0; b < 0;
D. a > 0; c <0.
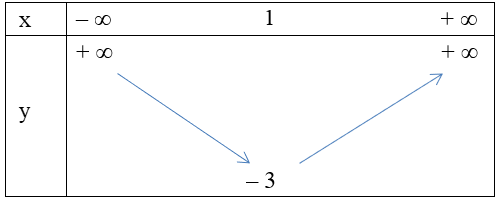
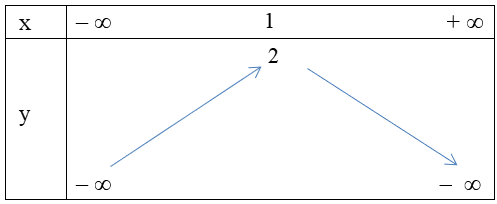
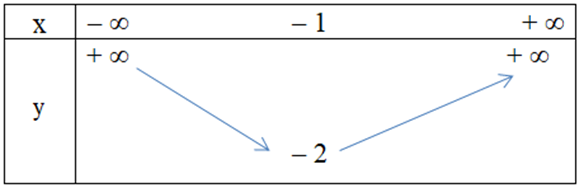
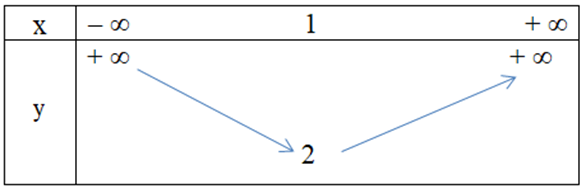
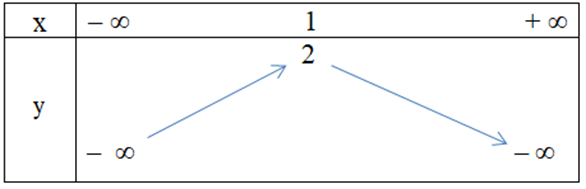
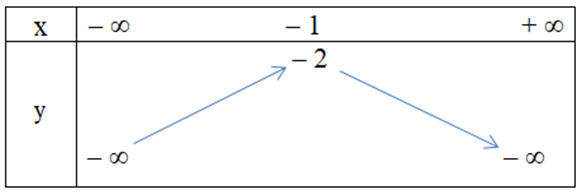
Câu 9. Hàm số y = x2 + 2x – 1 có bảng biến thiên là
A. 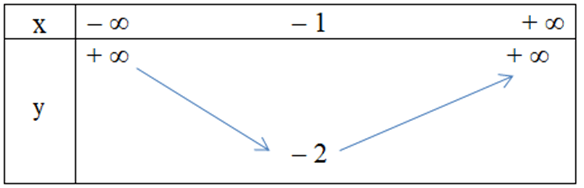
B. 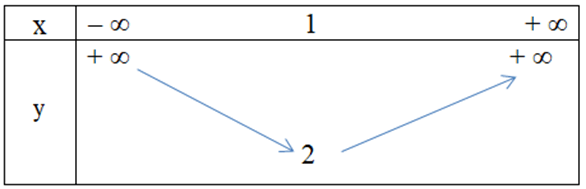
C.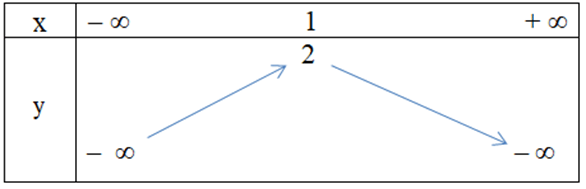
D.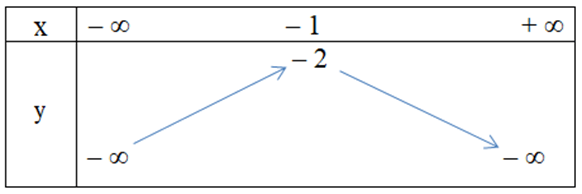
Câu 10. Đồ thị hàm số y = 4x2 – 3x – 1 có dạng nào trong các dạng sau đây?
A. 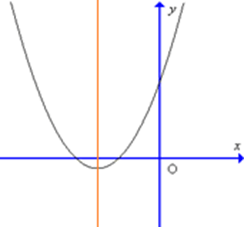
B. 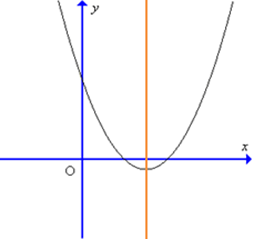
C. 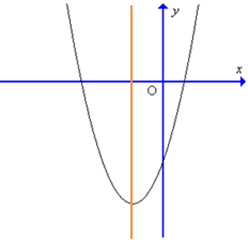
D. 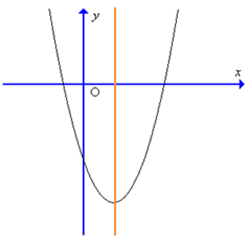
Câu 11. Parabol y = ax2 + bx + c đạt giá trị nhỏ nhất bằng 4 tại x = – 2 và đi qua
A(0; 6) có phương trình là
A.
B. y = x2 + 2x + 6
C. y = x2 + 6x + 6
D. y = x2 + x + 4
Câu 12. Cho hàm số y = f(x). Biết f(x + 2) = x2 – 3x + 2 thì f(x) bằng:
A. y = f(x) = x2 + 7x – 12;
B. y = f(x) = x2 – 7x – 12;
C. y = f(x) = x2 + 7x + 12;
D. y = f(x) = x2 – 7x + 12.
Câu 13. Cho hàm số y = ax2 + bx + c có đồ thị như hình dưới đây. Hàm số đó là hàm số nào?
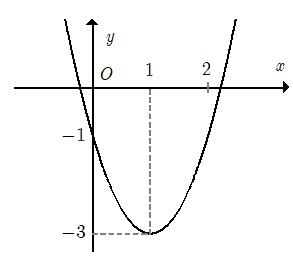
A. y = x2 – 4x – 1;
B. y = 2x2 – 4x – 1;
C. y = – 2x2 – 4x – 1;
D. y = 2x2 – 4x + 1.
Câu 14. Biết rằng P: y = ax2 + bx + 2 (a > 1) đi qua điểm M(–1; 6) và có tung độ đỉnh bằng . Tính tích P = a.b.
A. P = – 3
B. P = – 2
C. P = 192
D. P = 28
Câu 15. Biết rằng hàm số y = ax2 + bx + c (a ≠ 0) đạt cực đại bằng 3 tại x = 2 và có đồ thị hàm số đi qua điểm A(0; – 1). Tính tổng S = a + b + c.
A. S = – 1;
B. S = – 4;
C. S = 4;
D. S = 2.
Câu 1:
Trục đối xứng của parabol y = x2 – 4x + 1
A. x = 2;
B. x = – 2;
C. x = 4;
D. x = – 4.
Câu 2:
Tọa độ đỉnh I của hàm số y = – 3x2 + 4x – 1
A. \[{\rm{I}}\left( {--\frac{{\rm{2}}}{{\rm{3}}}{\rm{;}}\frac{{\rm{1}}}{{\rm{3}}}} \right)\];
B. \[{\rm{I}}\left( {\frac{{\rm{2}}}{{\rm{3}}}{\rm{;}}\frac{{\rm{1}}}{{\rm{3}}}} \right)\];
C. \[{\rm{I}}\left( {\frac{{\rm{4}}}{{\rm{3}}}{\rm{;}}--{\rm{1}}} \right)\];
D. \[{\rm{I}}\left( {\frac{2}{{\rm{3}}}{\rm{;}}\frac{4}{{\rm{3}}}} \right)\].
Câu 3:
Cho hàm số y = 2x2 – 4x – 1. Kết luận nào đúng trong các kết luận sau
A. Hàm số đồng biến trên khoảng (0; + ∞);
B. Hàm số đồng biến trên khoảng (– ∞; 1);
C. Hàm số nghịch biến trên khoảng (– ∞; 0);
D. Hàm số nghịch biến trên khoảng (– ∞; 2).
Câu 4:
Cho parabol y = ax2 + bx – 3. Xác định hệ số a, b biết parabol có đỉnh
I(– 1; – 5)
A. a = 1; b = 2;
B. a = 1; b = – 2;
C. a = – 2; b = 4;
D. a = 2; b = 4.
Câu 5:
Hàm số y = – x2 + 2x + 1 đồng biến trên khoảng
A. (– ∞; + ∞);
B. (– ∞; 1);
C. (1; + ∞);
D. (– ∞; 2).
Câu 6:
Cho parabol có đồ thị như hình sau:
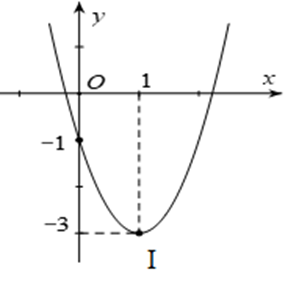
Tọa độ đỉnh I của parabol
A. I(– 1; – 3);
B. I(1; 0);
C. I(0; – 3);
D. I(1; – 3).
Câu 7:
Cho hàm số y = f(x) có đồ thị như hình sau:
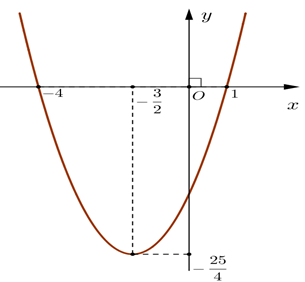
Hàm số đồng biến trên khoảng
A. \[\left( {--\infty {\rm{;}}--\frac{3}{2}} \right)\];
B. \[\left( {--\infty {\rm{;}}--\frac{{25}}{4}} \right)\];
C. \[\left( {--\frac{3}{2}; + \infty } \right)\];
D. \[\left( {--\frac{{{\rm{25}}}}{{\rm{4}}}; + \infty } \right)\].
Câu 8:
Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:
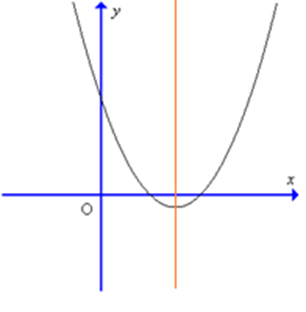
Kết luận nào sau đây đúng về hệ số a, b:
A. a > 0; b > 0;
B. a < 0; b > 0;
C. a > 0; b < 0;
D. a > 0; c <0.
Câu 10:
Đồ thị hàm số y = 4x2 – 3x – 1 có dạng nào trong các dạng sau đây?
A.
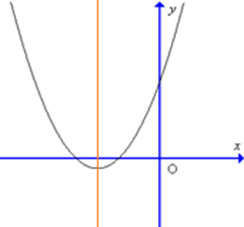
B.
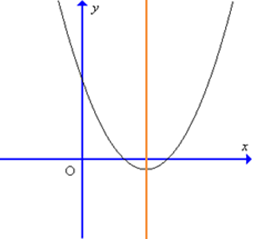
C.
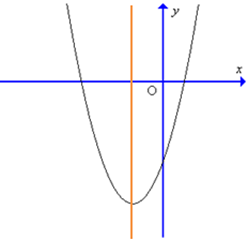
D.
Câu 11:
Parabol y = ax2 + bx + c đạt giá trị nhỏ nhất bằng 4 tại x = – 2 và đi qua
A(0; 6) có phương trình là
A. \[y = \frac{1}{2}{x^2} + 2x + 6\];
B. y = x2 + 2x + 6;
C. y = \(\frac{1}{2}\)x2 + 6x + 6;
D. y = x2 + x + 4.
Câu 12:
Cho hàm số y = f(x). Biết f(x + 2) = x2 – 3x + 2 thì f(x) bằng:
A. y = f(x) = x2 + 7x – 12;
B. y = f(x) = x2 – 7x – 12;
C. y = f(x) = x2 + 7x + 12;
D. y = f(x) = x2 – 7x + 12.
Câu 13:
Cho hàm số y = ax2 + bx + c có đồ thị như hình dưới đây. Hàm số đó là hàm số nào?
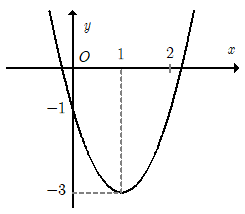
A. y = x2 – 4x – 1;
B. y = 2x2 – 4x – 1;
C. y = – 2x2 – 4x – 1;
D. y = 2x2 – 4x + 1.
Câu 14:
Biết rằng P: y = ax2 + bx + 2 (a > 1) đi qua điểm M(–1; 6) và có tung độ đỉnh bằng \( - \frac{1}{4}\). Tính tích P = a.b.
A. P = – 3;
B. P = – 2;
C. P = 192;
D. P = 28.
Câu 15:
Biết rằng hàm số y = ax2 + bx + c (a ≠ 0) đạt cực đại bằng 3 tại x = 2 và có đồ thị hàm số đi qua điểm A(0; – 1). Tính tổng S = a + b + c.
A. S = – 1;
B. S = – 4;
C. S = 4;
D. S = 2.