30 Bài tập trắc nghiệm tổng hợp Toán 10 Chương 6 Kết nối tri thức (có đáp án)
Với 30 bài tập trắc nghiệm tổng hợp Toán 10 Chương 6: Hàm số, đồ thị và ứng dụng có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
30 Bài tập trắc nghiệm tổng hợp Toán 10 Chương 6 Kết nối tri thức (có đáp án)
Câu 1. Tập xác định của hàm số là
A. ∅;
B. ℝ;
C. ℝ\{1};
D. ℝ\{0; 1}.
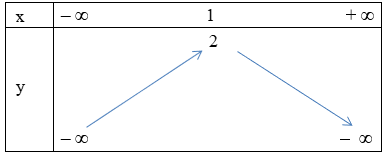
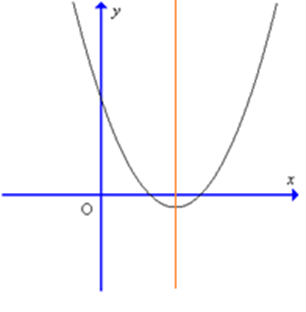
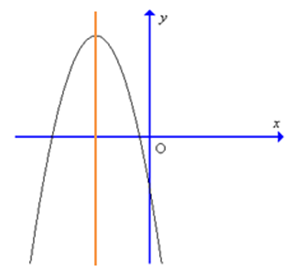
Câu 2. Cho hàm số có đồ thị như hình vẽ
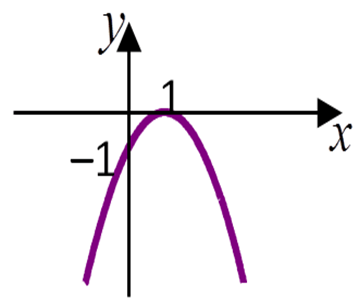
Kết luận nào sau đây là đúng
A. Hàm số nghịch biến trên khoảng (– ∞; – 1);
B. Hàm số đồng biến trên khoảng (1; + ∞);
C. Hàm số đồng biến trên khoảng (– ∞; 1);
D. Hàm số nghịch biến trên khoảng (– 1; + ∞).
Câu 3. Tọa độ đỉnh I của parabol (P): y = x2 + 8x + 12 là
A. I(– 4; – 4);
B. I(– 1; – 1);
C. I(– 4; 4);
D. I(4; 4).
Câu 4. Đồ thị hàm số y = – 9x2 + 6x – 1 có dạng là:
A. 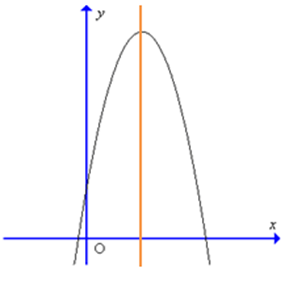
B.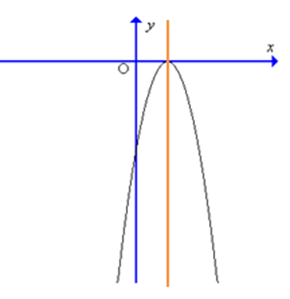
C.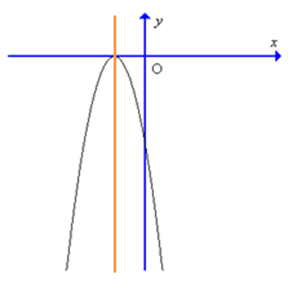
D.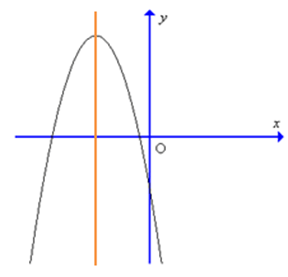
Câu 5. Cho f(x) = x2 – 1. Tìm khẳng định sai trong các khẳng định sau đây
A. f(x) < 0 khi x ∈ (– 1; 1);
B. f(x) > 0 khi x ∈ (– ∞; –1) (1; + ∞)
C. f(x) = 0 khi x = 1; x = – 1;
D. f(x) > 0 khi x ∈ (– 1; 1);
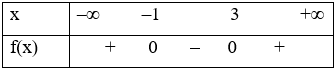
Câu 6. Tam thức f(x) = x2 – 2x – 3 nhận giá trị dương khi và chỉ khi
A. x ∈ (– ∞; – 3) (– 1; + ∞) ;
B. x ∈ (– ∞; – 1) (3; + ∞) ;
C. x ∈ (– ∞; – 2) (6; + ∞) ;
D. x ∈ (1; 3).
Câu 7. Cho parabol (P): y = ax2 + bx + 1. Xác định (P) biết rằng parabol đi qua hai điểm A(1; 4) và B(– 1; 2).
A. y = x2 + 2x + 1 ;
B. y = 5x2 – 2x + 1 ;
C. y = – x2 + 5x + 1 ;
D. y = 2x2 + x + 1 .
Câu 8. Nghiệm của phương trình
A. 5;
B. – 3;
C. 6;
D. 4.
Câu 9. Số nghiệm của phương trình
A. 4;
B. 2;
C. 0;
D. 1.
Câu 10. Tập xác định của hàm số y = là:
A. D = [2; + ∞);
B. D = [2; 6) ∪ (6; + ∞)
C. D = (6; + ∞);
D. D = ℝ\{6}.
Câu 11. Cho parabol (P): y = ax2 + bx + c có đồ thị như hình bên. Phương trình của parabol này là :
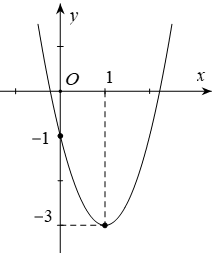
A. y = 2x2 – 4x – 1;
B. y = x2 – 2x – 1;
C. y = 2x2 – 8x – 1;
D. y = 2x2 – x – 1.
Câu 12. Cho hàm số: y = x2 – 2x – 1, khẳng định nào sau đây sai?
A. Hàm số đồng biến trên (1; + ∞) ;
B. Đồ thị hàm số có trục đối xứng x = – 2;
C. Hàm số nghịch biến trên (– ∞; 1);
D. Đồ thị hàm số có đỉnh I(1; – 2).
Câu 13. Cho f(x) = mx2 – 2x – 1. Xác định m để f(x) < 0 với mọi x ∈ ℝ.
A. m < – 1;
B. m < 0;
C. – 1 < m < 0.
D. m < 1 và m ≠ 0.
Câu 14. Tổng các nghiệm của phương trình là:
A. 1;
B. 0;
C. 2;
D.
Câu 15. Nghiệm của phương trình là
A. x = 2;
B. x = 4;
C. x = 5;
D. x = 6.
Câu 16. Hàm số y = – x2 + 2x + 1 đồng biến trên khoảng
A. (– ∞; + ∞);
B. (– ∞; 1);
C. (1; + ∞);
D. (– ∞; 2).
Câu 17. Cho bất phương trình 2x2 – 4x + m + 5 > 0. Tìm m để bất phương trình đúng ?
A. m ≥ – 11;
B. m > – 11;
C. m < – 11;
D. m < 11.
Câu 18. Tập ngiệm của bất phương trình: x(x + 5) ≤ 2(x2 + 2) là:
A.
B.
C.
D.
Câu 19. Bất phương trình: có bao nhiêu nghiệm nguyên dương?
A. 0
B. 1
C. 2
D. 3
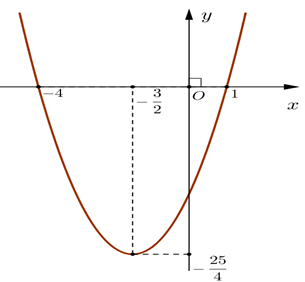
Câu 20. Cho hàm số y = f(x) có đồ thị như hình sau:
Hàm số đồng biến trên khoảng
A.
B.
C.
D.
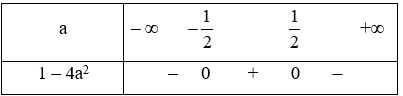
Câu 21. Tìm tất cả các giá trị của a để bất phương trình ax2 – x + a ≥ 0,
A. a = 0;
B. a < 0;
C.
D.
Câu 22. Để f(x) = x2 + (m + 1)x +2m + 7 > 0 với mọi x thì
A. – 3 ≤ m ≤ 9;
B.
C. – 3 < m < 9;
D.
Câu 23. Tìm tất cả các giá trị thực của tham số m để bất phương trình
f(x) = (m – 3)x2 + (m + 2)x – 4 > 0 vô nghiệm
A.
B. – 22 ≤ m ≤ 2;
C. – 22 < m < 2;
D.
Câu 24. Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:
Kết luận nào sau đây đúng về hệ số a, b:
A. a > 0; b > 0;
B. a < 0; b > 0;
C. a > 0; b < 0;
D. a > 0; c <0.
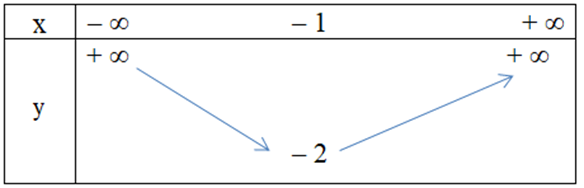
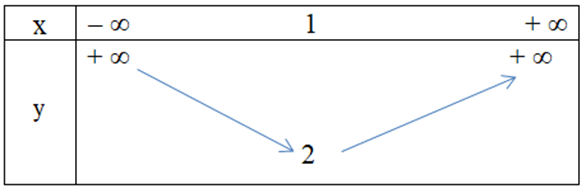
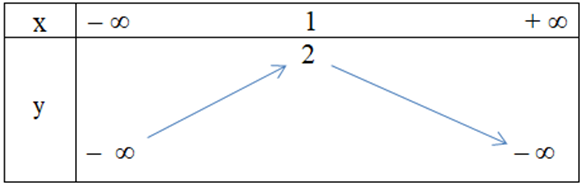
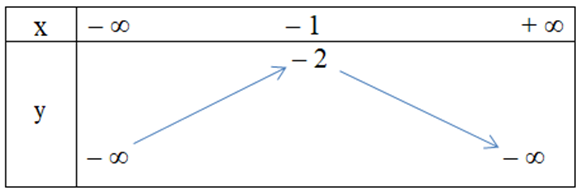
Câu 25. Hàm số y = x2 + 2x – 1 có bảng biến thiên là
A.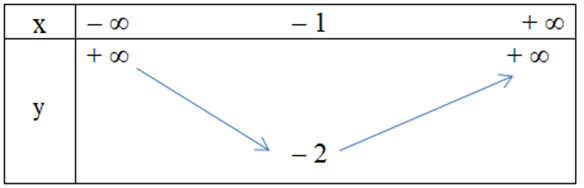
B. 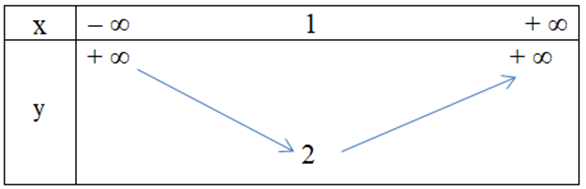
C.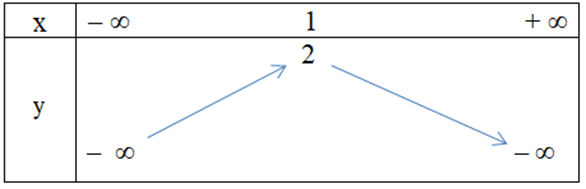
D.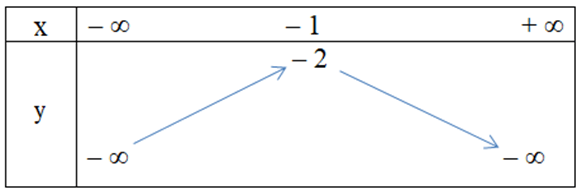
Câu 26. Đồ thị hàm số y = 4x2 – 3x – 1 có dạng nào trong các dạng sau đây?
A.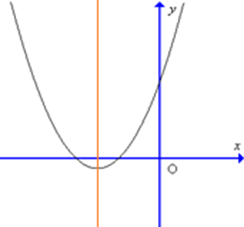
B.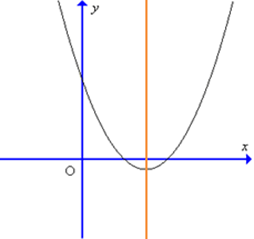
C.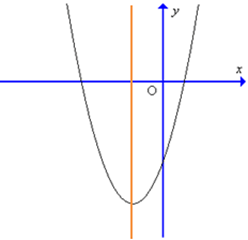
D.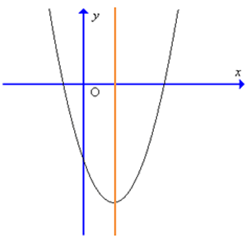
Câu 27. Tập xác định của hàm số là
A. [2; +∞)
B. [1; +∞)
C.
D.
Câu 28. Phương trình x2 – (m – 1)x + m2 – 3m + 2 = 0 có hai nghiệm trái dấu nhau khi và chỉ khi
A. m < 3;
B. m < 1;
C. m = 1;
D. 1 < m < 2.
Câu 29. Số giá trị nguyên của x thỏa mãn điều kiện xác định của phương trình : là:
A. 0
B. 1
C. 2
D. 3
Câu 30. Phương trình có bao nhiêu nghiệm nguyên âm:
A. 0
B. 1
C. 2
D. 3
Câu 1:
Tập xác định của hàm số \[y = \frac{{x - 1}}{{{x^2} - x + 3}}\] là
A. \[\emptyset \];
B. ℝ;
C. ℝ\{1};
D. ℝ\{0; 1}.
Câu 2:
Cho hàm số có đồ thị như hình vẽ

Kết luận nào sau đây là đúng
A. Hàm số nghịch biến trên khoảng (– ∞; – 1);
B. Hàm số đồng biến trên khoảng (1; + ∞);
C. Hàm số đồng biến trên khoảng (– ∞; 1);
D. Hàm số nghịch biến trên khoảng (– 1; + ∞).
Câu 3:
Tọa độ đỉnh I của parabol (P): y = x2 + 8x + 12 là
A. I(– 4; – 4);
B. I(– 1; – 1);
C. I(– 4; 4);
D. I(4; 4).
Câu 5:
Cho f(x) = x2 – 1. Tìm khẳng định sai trong các khẳng định sau đây
A. f(x) < 0 khi x ∈ (– 1; 1);
B. f(x) > 0 khi x ∈ (– ∞; –1) \( \cup \) (1; + ∞)
C. f(x) = 0 khi x = 1; x = – 1;
D. f(x) > 0 khi x ∈ (– 1; 1);
Câu 6:
Tam thức f(x) = x2 – 2x – 3 nhận giá trị dương khi và chỉ khi
A. x ∈ (– ∞; – 3) \( \cup \) (– 1; + ∞);
B. x ∈ (– ∞; – 1) \( \cup \) (3; + ∞);
C. x ∈ (– ∞; – 2) \( \cup \) (6; + ∞);
D. x ∈ (1; 3).
Câu 7:
Cho parabol (P): y = ax2 + bx + 1. Xác định (P) biết rằng parabol đi qua hai điểm A(1; 4) và B(– 1; 2).
A. y = x2 + 2x + 1;
B. y = 5x2 – 2x + 1;
C. y = – x2 + 5x + 1;
D. y = 2x2 + x + 1.
Câu 9:
Số nghiệm của phương trình \[\sqrt {{x^2} - 3x} = \sqrt {2x - 4} \]
A. 4;
B. 2;
C. 0;
D. 1.
Câu 10:
A. D = [2; + ∞);
B. D = [2; 6) \[ \cup \] (6; + ∞)
C. D = (6; + ∞);
D. D = ℝ\{6}.
Câu 11:
Cho parabol (P): y = ax2 + bx + c có đồ thị như hình bên. Phương trình của parabol này là :
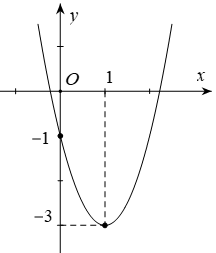
A. y = 2x2 – 4x – 1;
B. y = x2 – 2x – 1;
C. y = 2x2 – 8x – 1;
D. y = 2x2 – x – 1.
Câu 12:
A. Hàm số đồng biến trên (1; + ∞) ;
B. Đồ thị hàm số có trục đối xứng x = – 2;
C. Hàm số nghịch biến trên (– ∞; 1);
D. Đồ thị hàm số có đỉnh I(1; – 2).
Câu 13:
Cho f(x) = mx2 – 2x – 1. Xác định m để f(x) < 0 với mọi x ∈ ℝ.
A. m < – 1;
B. m < 0;
C. – 1 < m < 0.
D. m < 1 và m ≠ 0.
Câu 14:
Tổng các nghiệm của phương trình \[{x^2} - 2x + 3\sqrt {{x^2} - 2x - 3} = 7\] là:
A. 1;
B. 0;
C. 2;
D. \[2\sqrt 2 \].
Câu 15:
Nghiệm của phương trình \[\sqrt {x - 2} + \sqrt {x + 3} = 5\] là
A. x = 2;
B. x = 4;
C. x = 5;
D. x = 6.
Câu 16:
Hàm số y = – x2 + 2x + 1 đồng biến trên khoảng
A. (– ∞; + ∞);
B. (– ∞; 1);
C. (1; + ∞);
D. (– ∞; 2).
Câu 17:
Cho bất phương trình 2x2 – 4x + m + 5 > 0. Tìm m để bất phương trình đúng \(\forall x \ge 3\)?
A. m ≥ – 11;
B. m > – 11;
C. m < – 11;
D. m < 11.
Câu 18:
Tập ngiệm của bất phương trình: x(x + 5) ≤ 2(x2 + 2) là:
A. \[(--\infty ;1] \cup [4; + \infty )\] ;
B. \(\left[ {1;4} \right]\) ;
C. \[(--\infty ;1) \cup (4; + \infty )\];
D. \((1;4)\).
Câu 19:
Bất phương trình: \[\left( {{x^2} - 3x - 4} \right).\sqrt {{x^2} - 5} < 0\] có bao nhiêu nghiệm nguyên dương?
A. 0;
B. 1;
C. 2;
D. 3.
Câu 20:
Cho hàm số y = f(x) có đồ thị như hình sau:
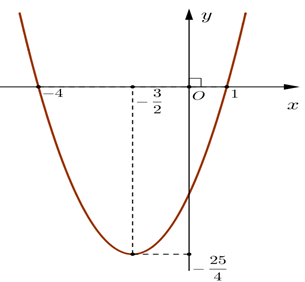
Hàm số đồng biến trên khoảng
A. \[\left( {--\infty {\rm{;}}--\frac{3}{2}} \right)\];
B. \[\left( {--\infty {\rm{;}}--\frac{{25}}{4}} \right)\];
C. \[\left( {--\frac{3}{2}; + \infty } \right)\];
D. \[\left( {--\frac{{{\rm{25}}}}{{\rm{4}}}; + \infty } \right)\].
Câu 21:
Tìm tất cả các giá trị của a để bất phương trình ax2 – x + a ≥ 0, \(\forall x \in \mathbb{R}\)
A. a = 0;
B. a < 0;
C. \(0 < a \le \frac{1}{2}\).
D. \(a \ge \frac{1}{2}\).
Câu 22:
Để f(x) = x2 + (m + 1)x +2m + 7 > 0 với mọi x thì
A. – 3 ≤ m ≤ 9;
B. \(\left[ \begin{array}{l}m < - 3\\m > 9\end{array} \right.\).
C. – 3 < m < 9;
D. \(\left[ \begin{array}{l}m \le - 3\\m \ge 9\end{array} \right.\).
Câu 23:
Tìm tất cả các giá trị thực của tham số m để bất phương trình
f(x) = (m – 3)x2 + (m + 2)x – 4 > 0 vô nghiệm
C. – 22 < m < 2;
D. \[\left[ \begin{array}{l} - 22 \le m \le 2\\m = 3\end{array} \right.\].
Câu 24:
Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:
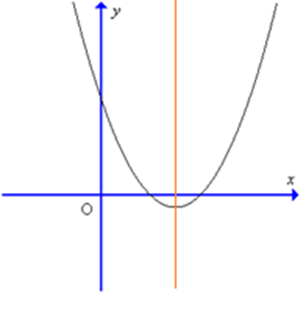
Kết luận nào sau đây đúng về hệ số a, b:
A. a > 0; b > 0;
B. a < 0; b > 0;
C. a > 0; b < 0;
D. a > 0; c <0.
Câu 26:
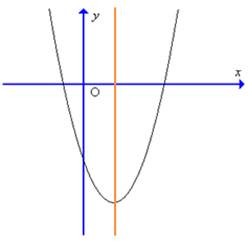
Đồ thị hàm số y = 4x2 – 3x – 1 có dạng nào trong các dạng sau đây?
A.
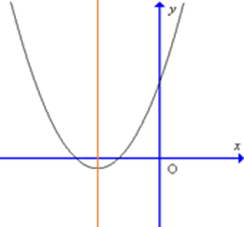
B.
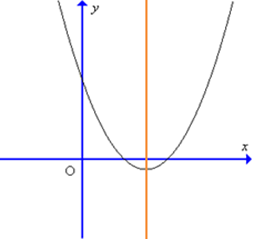
C.
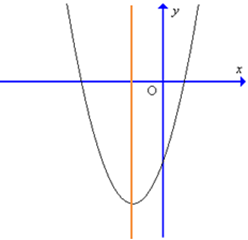
D.
Câu 27:
Tập xác định của hàm số \[y = \sqrt {x - 2} + \frac{{\sqrt {{x^2} - 1} }}{3}\] là
A. [2; +∞);
B. [1; +∞);
C. \[\left( { - \infty ;1} \right] \cup \left[ {2; + \infty } \right)\];
D. \[\left( {1;2} \right) \cup \left( {3; + \infty } \right)\].
Câu 28:
Phương trình x2 – (m – 1)x + m2 – 3m + 2 = 0 có hai nghiệm trái dấu nhau khi và chỉ khi
A. m < 3;
B. m < 1;
C. m = 1;
D. 1 < m < 2.
Câu 29:
Số giá trị nguyên của x thỏa mãn điều kiện xác định của phương trình :\(\sqrt {2 - x} + \frac{4}{{\sqrt {x + 1} + 3}} = 1\) là:
A. 0;
B. 1;
C. 2;
D. 3.
Câu 30:
Phương trình \[(x + 4)(x + 1) - 3\sqrt {{x^2} + 5x + 2} = 6\] có bao nhiêu nghiệm nguyên âm:
A. 0;
B. 1;
C. 2;
D. 3;