Bài 4 trang 77 Toán 11 Tập 1 Cánh diều
Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:
Giải Toán 11 Bài 3: Hàm số liên tục - Cánh diều
Bài 4 trang 77 Toán 11 Tập 1: Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:
a) f(x) = x2 + sinx;
b) g(x) = x4 – x2 + ;
c) h(x) = .
Lời giải:
a) Hàm số f(x) = x2 + sinx có tập xác định là ℝ.
Hàm số x2 và sinx liên tục trên ℝ nên hàm số f(x) = x2 + sinx liên tục trên ℝ.
b) Hàm số g(x) = x4 – x2 + có tập xác định là ℝ\{1}.
Hàm số x4 – x2 liên tục trên toàn bộ tập xác định
Hàm số liên tục trên các khoảng ( – ∞; 1) và (1; +∞).
Vậy hàm số đã cho liên tục trên từng khoảng xác định của hàm số.
c) Hàm số h(x) = có tập xác định D = ℝ\{– 4; 3}.
Hàm số liên tục trên các khoảng ( – ∞; 3) và (3; +∞).
Hàm số liên tục trên các khoảng ( – ∞; – 4) và (– 4; +∞).
Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:
Hoạt động 1 trang 73 Toán 11 Tập 1: Quan sát đồ thị hàm số f(x) = x ở Hình 11 ....
Luyện tập 1 trang 74 Toán 11 Tập 1: Xét tính liên tục của hàm số f(x) = x3 + 1 tại x0 = 1 ....
Hoạt động 2 trang 74 Toán 11 Tập 1: Cho hàm số f(x) = x + 1 với x ∈ ℝ ....
Luyện tập 2 trang 75 Toán 11 Tập 1: Hàm số f(x) =
. Có liên tục trên ℝ hay không? ....
Hoạt động 3 trang 75 Toán 11 Tập 1: Quan sát đồ thị các hàm số: y = x2 – 4x + 3 (Hình 14a) ....
Luyện tập 3 trang 76 Toán 11 Tập 1: Hàm f(x)=có liên tục trên mỗi khoảng (– ∞; 8) ....

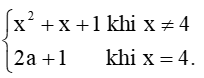 ....
....