Luyện tập 3 trang 93 Toán 11 Tập 2 Cánh diều
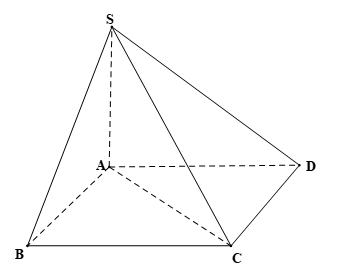
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA ⊥ (ABCD). Tính số đo của mỗi góc nhị diện sau:
Giải Toán 11 Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện - Cánh diều
Luyện tập 3 trang 93 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA ⊥ (ABCD). Tính số đo của mỗi góc nhị diện sau:
a) [B, SA, D];
b) [B, SA, C].
Lời giải:
a) Ta có: SA ⊥ (ABCD) và AB ⊂ (ABCD), AD ⊂ (ABCD).
Suy ra: SA ⊥ AB, SA ⊥ AD.
Mà AB ∩ AD = A ∈ SA.
Do đó là góc phẳng nhị diện của góc nhị diện [B, SA, D].
Vì ABCD là hình vuông nên
Vậy số đo của góc nhị diện [B, SA, D] bằng 90°.
b) Do SA ⊥ (ABCD) và AC ⊂ (ABCD) nên SA ⊥ AC.
Ta có: SA ⊥ AC, SA ⊥ AB (theo câu a) và AC ∩ AB = A ∈ SA.
Do đó là góc phẳng nhị diện của góc nhị diện [B, SA, C].
Vì ABCD là hình vuông nên đường chéo AC là đường phân giác của góc BAD, do đó
Vậy số đo của góc nhị diện [B, SA, C] = 45°.
Lời giải bài tập Toán 11 Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện hay, chi tiết khác: