Giải Toán 11 trang 106 Tập 2 Cánh diều

---

Haylamdo biên soạn và sưu tầm lời giải Toán 11 trang 106 Tập 2 trong Bài 5: Khoảng cách Toán 11 Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 11 dễ dàng làm bài tập Toán 11 trang 106.

Giải Toán 11 trang 106 Tập 2 Cánh diều

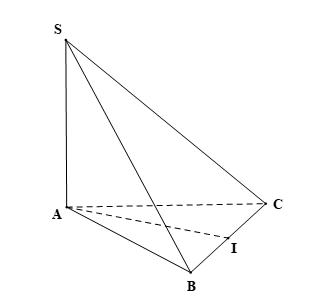
Luyện tập 5 trang 106 Toán 11 Tập 2: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC). Tính d(SA, BC).

Lời giải:

Gọi I là trung điểm của BC.

Xét ∆ABC đều có: AI là đường trung tuyến (do I là trung điểm của BC).

Suy ra AI ⊥ BC.

Do SA ⊥ (ABC) và AI ⊂ (ABC) nên SA ⊥ AI.

Ta có: AI ⊥ SA và AI ⊥ BC.

Suy ra đoạn thẳng AI là đoạn vuông góc chung của hai đường thẳng SA và BC.

Từ đó ta có d(SA, BC) = AI.

Xét ∆ABC đều cạnh a, có I là trung điểm của BC nên $BI=\frac{BC}{2}=\frac{a}{2}.$

Áp dụng định lí Pythagore vào tam giác ABI vuông tại I (do AI ⊥ BC) có:

AB² = AI² + BI²

Suy ra $AI=\sqrt{A{B}^2-B{I}^2}=\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{3}}{2}.$

Vậy $d\left(SA,BC\right)=AI=\frac{a\sqrt{3}}{2}.$

Bài 1 trang 106 Toán 11 Tập 2: Hình 76 gợi nên hình ảnh hai mặt phẳng (P) và (Q) song song với nhau. Cột gỗ cao 4,2 m. Khoảng cách giữa (P) và (Q) là bao nhiêu mét?

Lời giải:

Do hai mặt phẳng (P) và (Q) song song với nhau nên khoảng cách giữa (P) và (Q) bằng chiều cao của cột gỗ.

Vậy khoảng cách giữa (P) và (Q) bằng 4,2 m.

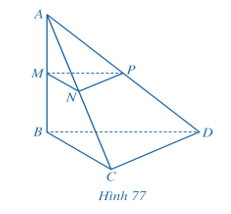
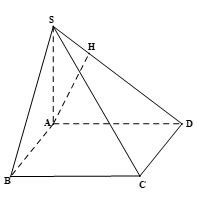
Bài 2 trang 106 Toán 11 Tập 2: Cho hình tứ diện ABCD có AB = a, BC = b, BD = c, $\widehat{ABC}=\widehat{ABD}=\widehat{BCD}=90°.$ Gọi M, N, P lần lượt là trung điểm của AB, AC, AD (Hình 77).

a) Tính khoảng cách từ điểm C đến đường thẳng AB.

b) Tính khoảng cách từ điểm D đến mặt phẳng (ABC).

c) Tính khoảng cách giữa hai đường thẳng AB và CD.

Lời giải:

a) Vì $\widehat{ABC}=90°$ nên CB ⊥ AB.

Suy ra d(C, AB) = CB = b.

Vậy khoảng cách từ điểm C đến đường thẳng AB bằng b.

b) Vì $\widehat{ABD}=90°$ nên AB ⊥ BD.

Ta có: AB ⊥ CB, AB ⊥ BD và CB ∩ BD = B trong (BCD).

Suy ra AB ⊥ (BCD).

Mà CD ⊂ (BCD) nên AB ⊥ CD.

Vì $\widehat{BCD}=90°$ nên CD ⊥ BC.

Ta có: CD ⊥ AB, CD ⊥ BC và AB ∩ BC = B trong (ABC).

Suy ra CD ⊥ (ABC).

Khi đó d(D, (ABC)) = CD.

Áp dụng định lí Pythagore vào tam giác BCD vuông tại C có:

BD² = BC² + CD²

Suy ra $CD=\sqrt{B{D}^2-B{C}^2}=\sqrt{c^2-b^2}.$

Do đó $d\left(D,\left(ABC\right)\right)=CD=\sqrt{c^2-b^2}.$

Vậy khoảng cách từ điểm D đến mặt phẳng (ABC) bằng $\sqrt{c^2-b^2}.$

c) Ta có: BC ⊥ AB (theo câu a) và BC ⊥ CD (theo câu b).

Suy ra đoạn thẳng BC là đoạn vuông góc chung của hai đường thẳng AB và CD.

Do đó d(AB, CD) = BC = b.

Vậy khoảng cách giữa hai đường thẳng AB và CD bằng b.

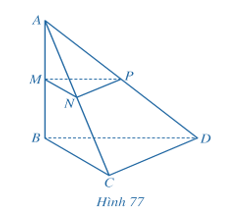
Bài 3 trang 106 Toán 11 Tập 2: Với giả thiết ở Bài tập 2, hãy:

a) Chứng minh rằng MN // BC. Tính khoảng cách giữa hai đường thẳng MN và BC.

b) Chứng minh rằng MP // (BCD). Tính khoảng cách từ đường thẳng MP đến mặt phẳng (BCD).

c) Chứng minh rằng (MNP) // (BCD). Tính khoảng cách giữa hai mặt phẳng (MNP) và (BCD).

Lời giải:

a) Xét ∆ABC có: M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của ∆ABC.

Do đó MN // BC.

Do đó d(MN, BC) = d(M, BC).

Mà AB ⊥ BC (theo câu a Bài tập 2) nên MB ⊥ BC, do đó d(M, BC) = MB.

Khi đó, $d\left(MN,BC\right)=MB=\frac{AB}{2}=\frac{a}{2}$ (do M là trung điểm của AB).

Vậy khoảng cách giữa hai đường thẳng MN và BC bằng $\frac{a}{2}.$

d) Xét ∆ABD có: M, P lần lượt là trung điểm của AB và AD nên MP là đường trung bình của ∆ABD.

Do đó MP // BD.

Mà BD ⊂ (BCD) nên MP // (BCD).

Suy ra d(MP, (BCD)) = d(M, (BCD)).

Ta có: AB ⊥ (BCD) (theo câu b Bài tập 2) mà M ∈ AB nên MB ⊥ (ABC).

Suy ra $d\left(M,\left(BCD\right)\right)=MB=\frac{a}{2}.$

Nên $d\left(MP,\left(BCD\right)\right)=d\left(M,\left(BCD\right)\right)=\frac{a}{2}.$

Vậy khoảng cách từ đường thẳng MP đến mặt phẳng (BCD) bằng $\frac{a}{2}.$

c) Do MN // BC và BC ⊂ (BCD) nên MN // (BCD).

Ta có: MN // (BCD), MP // (BCD) và MN ∩ MP = M trong (MNP).

Suy ra (MNP) // (BCD).

Do đó $d\left(\left(MNP\right),\left(BCD\right)\right)=d\left(M,\left(BCD\right)\right)=MB=\frac{a}{2}.$

Vậy khoảng cách giữa hai mặt phẳng (MNP) và (BCD) bằng $\frac{a}{2}.$

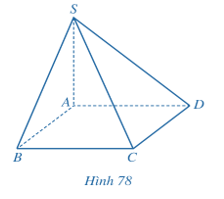
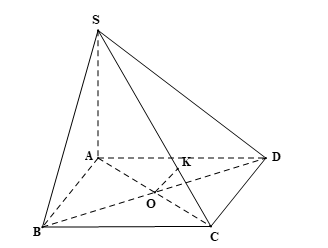
Bài 4 trang 106 Toán 11 Tập 2: Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình vuông cạnh a, SA = a (Hình 78).

a) Tính khoảng cách từ điểm S đến đường thẳng CD.

b) Tính khoảng cách từ điểm D đến mặt phẳng (SAB).

c) Tính khoảng cách từ điểm A đến mặt phẳng (SCD).

Lời giải:

a) Do SA ⊥ (ABCD) và CD ⊂ (ABCD) nên SA ⊥ CD.

Vì ABCD là hình vuông nên CD ⊥ AD.

Ta có: CD ⊥ SA, CD ⊥ AD và SA ∩ AD = A trong (SAD).

Suy ra CD ⊥ (SAD).

Mà SD ⊂ (SAD) nên CD ⊥ SD.

Suy ra d(S, CD) = SD.

Do SA ⊥ (ABCD) và AD ⊂ (ABCD) nên SA ⊥ AD.

Áp dụng định lí Pythagore vào tam giác SAD vuông tại A (do SA ⊥ AD) có:

SD² = SA² + AD² = a² + a² = 2a².

Suy ra $SD=a\sqrt{2}.$

Do đó $d\left(S,CD\right)=SD=a\sqrt{2}.$

Vậy khoảng cách từ điểm S đến đường thẳng CD bằng $a\sqrt{2}.$

b) Vì ABCD là hình vuông nên AD ⊥ AB.

Ta có: AD ⊥ SA (theo câu a), AD ⊥ AB và SA ∩ AB = A trong (SAB).

Suy ra AD ⊥ (SAB).

Khi đó d(D, (SAB)) = AD = a.

Vậy khoảng cách từ điểm D đến mặt phẳng (SAB) bằng a.

c) Kẻ AH ⊥ SD (H ∈ SD).

Do CD ⊥ (SAD) (theo câu a) và AH ⊂ (SAD) nên CD ⊥ AH.

Ta có: AH ⊥ CD, AH ⊥ SD và CD ∩ SD = D trong (SCD).

Suy ra AH ⊥ (SCD).

Khi đó d(A, (SCD)) = AH.

Áp dụng hệ thức lượng trong tam giác SAD vuông tại A, đường cao AH có:

$\frac{1}{A{H}^2}=\frac{1}{S{A}^2}+\frac{1}{A{D}^2}$$=\frac{1}{a^2}+\frac{1}{a^2}=\frac{2}{a^2}$

Suy ra $AH=\frac{a\sqrt{2}}{2}.$

Do đó $d\left(A,\left(SCD\right)\right)=AH=\frac{a\sqrt{2}}{2}.$

Vậy khoảng cách từ điểm A đến mặt phẳng (SCD) bằng $\frac{a\sqrt{2}}{2}.$

Bài 5 trang 106 Toán 11 Tập 2: Với giả thiết ở Bài tập 4, hãy:

a) Chứng minh rằng BC // (SAD) và tính khoảng cách giữa BC và mặt phẳng (SAD).

b) Chứng minh rằng BD ⊥ (SAC) và tính khoảng cách giữa hai đường thẳng BD và SC.

Lời giải:

a) Do ABCD là hình vuông nên BC // AD.

Mà AD ⊂ (SAD) nên BC // (SAD).

Khi đó, d(BC, (SAD)) = d(C, (SAD)) = CD = a.

(vì theo câu a, CD ⊥ (SAD))

Vậy khoảng cách giữa BC và mặt phẳng (SAD) bằng a.

b) Vì ABCD là hình vuông nên BD ⊥ AC.

Do SA ⊥ (ABCD) và BD ⊂ (ABCD) nên SA ⊥ BD.

Ta có: BD ⊥ SA, BD ⊥ AC và SA ∩ AC = A trong (SAC).

Suy ra BD ⊥ (SAC).

Gọi O = AC ∩ BD, kẻ OK ⊥ SC (K ∈ SC).

Do BD ⊥ (SAC) và OK ⊂ (SAC) nên BD ⊥ OK.

Ta có: OK ⊥ SC và OK ⊥ BD.

Từ đó ta có đoạn thẳng OK là đoạn vuông góc chung của hai đường thẳng BD và SC nên d(BD, SC) = OK.

Do ABCD là hình vuông nên $\widehat{ABC}=90°,$ do đó tam giác ABC vuông tại B.

Áp dụng định lí Pythagore trong tam giác ABC vuông tại B có:

AC² = AB² + BC² = a² + a² = 2a².

Suy ra $AC=a\sqrt{2}.$

Do O = AC ∩ BD và AC, BD là hai đường chéo của hình vuông ABCD.

Suy ra O là trung điểm của AC nên $OC=\frac{AC}{2}=\frac{a\sqrt{2}}{2}.$

Do SA ⊥ (ABCD) và AC ⊂ (ABCD) nên SA ⊥ AC.

Áp dụng định lí Pythagore trong tam giác SAC vuông tại A (do SA ⊥ AC) có:

SC² = SA² + AC².

Do đó $SC=\sqrt{a^2+{\left(a\sqrt{2}\right)}^2}=\sqrt{a^2+2a^2}=a\sqrt{3}.$

Xét ∆SAC và ∆OKC có:

$\widehat{SAC}=\widehat{OKC}=90°;$

$\widehat{OCK}$ là góc chung

Do đó ∆SAC ᔕ ∆OKC (g.g).

Suy ra $\frac{SA}{OK}=\frac{SC}{OC}$ (tỉ số đồng dạng)

Nên $OK=\frac{SA.OC}{SC}=\frac{a.\frac{a\sqrt{2}}{2}}{a\sqrt{3}}=\frac{a\sqrt{6}}{6}.$

Khi đó $d\left(BD,SC\right)=OK=\frac{a\sqrt{6}}{6}.$

Vậy khoảng cách giữa hai đường thẳng BD và SC $\frac{a\sqrt{6}}{6}.$

Lời giải bài tập Toán 11 Bài 5: Khoảng cách hay khác:

• Giải Toán 11 trang 101
• Giải Toán 11 trang 102
• Giải Toán 11 trang 103
• Giải Toán 11 trang 104