Giải Toán 11 trang 112 Tập 2 Cánh diều

---

Haylamdo biên soạn và sưu tầm lời giải Toán 11 trang 112 Tập 2 trong Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối Toán 11 Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 11 dễ dàng làm bài tập Toán 11 trang 112.

Giải Toán 11 trang 112 Tập 2 Cánh diều

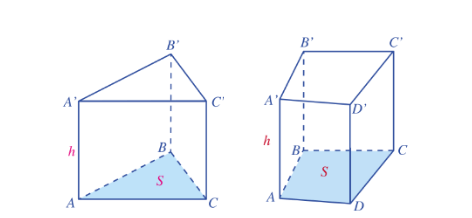
Hoạt động 4 trang 112 Toán 11 Tập 2: Hãy nêu lại công thức tính thể tích của khối lăng trụ đứng tam giác, khối lăng trụ đứng tứ giác.

Lời giải:

Thể tích của khối lăng trụ đứng tam giác, tứ giác đều được tính bằng công thức:

V = S.h.

 Trong đó S là diện tích đáy và h là chiều cao khối lăng trụ đứng tam giác.

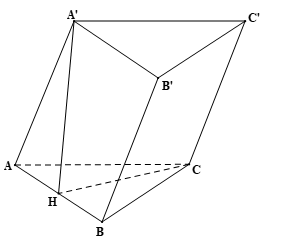
Luyện tập 4 trang 112 Toán 11 Tập 2: Tính thể tích của khối lăng trụ ABC.A’B’C’ biết tất cả các cạnh bằng a và hình chiếu của A’ trên mặt phẳng (ABC) là trung điểm của AB.

Lời giải:

Gọi H là trung điểm của AB nên $AH=\frac{AB}{2}=\frac{a}{2}.$

Vì hình chiếu của A’ trên mặt phẳng (ABC) là trung điểm của AB nên A’H ⊥ (ABC).

Ta có: A’H ⊥ (ABC) và AB ⊂ (ABC) nên A’H ⊥ AB.

Áp dụng định lí Pythagore vào tam giác A’AH vuông tại H (do A’H ⊥ AB) có:

A’A² = A’H² + AH²

Do đó $A^{\text{'}}H=\sqrt{A^{\text{'}}{A}^2-A{H}^2}=\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}=\sqrt{a^2-\frac{a^2}{4}}=\sqrt{\frac{3a^2}{4}}=\frac{a\sqrt{3}}{2}.$

Xét ∆ABC đều có: CH là đường trung tuyến (do H là trung điểm của AB) nên CH cũng là đường cao của tam giác ABC hay CH ⊥ AB.

Áp dụng định lí Pythagore vào tam giác ACH vuông tại H (do CH ⊥ AB) có:

AC² = AH² + CH²

Do đó $CH=\sqrt{A{C}^2-A{H}^2}=\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}=\sqrt{a^2-\frac{a^2}{4}}=\sqrt{\frac{3a^2}{4}}=\frac{a\sqrt{3}}{2}.$

Khi đó, diện tích tam giác ABC có đường cao $CH=\frac{a\sqrt{3}}{2}$ là:

$S_{\Delta ABC}=\frac{1}{2}CH.AB=\frac{1}{2}.\frac{a\sqrt{3}}{2}.a=\frac{a^2\sqrt{3}}{4}$ (đvdt)

Thể tích của khối lăng trụ ABC.A’B’C’ có chiều cao $A^{\text{'}}H=\frac{a\sqrt{3}}{2}$ và diện tích đáy $S_{\Delta ABC}=\frac{a^2\sqrt{3}}{4}$ là:

$V_{ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=S_{\Delta ABC}.A^{\text{'}}H=\frac{a^2\sqrt{3}}{4}\cdot \frac{a\sqrt{3}}{2}=\frac{3a^3}{8} \left(đvtt\right)$

Lời giải bài tập Toán 11 Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối hay khác:

• Giải Toán 11 trang 107
• Giải Toán 11 trang 110
• Giải Toán 11 trang 114
• Giải Toán 11 trang 115