Giải Toán 11 trang 12 Tập 1 Cánh diều

---

Với Giải Toán 11 trang 12 Tập 1 trong Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác Toán lớp 11 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 12.

Giải Toán 11 trang 12 Tập 1 Cánh diều

Luyện tập 9 trang 12 Toán 11 Tập 1: Cho góc lượng giác α sao cho $\pi <\alpha <\frac{3\pi }{2}$ và $\sin \alpha =-\frac{4}{5}$. Tìm cosα.

Lời giải:

Do $\pi <\alpha <\frac{3\pi }{2}$ nên cosα < 0.

Áp dụng công thức cos²α + sin²α= 1, ta có: $co{s}^2\alpha +{\left(-\frac{4}{5}\right)}^2=1$

Suy ra $co{s}^2\alpha =1-{\left(-\frac{4}{5}\right)}^2=1-\frac{16}{25}=\frac{9}{25}$

Do đó $cos\alpha =-\frac{3}{5}$(do cosα < 0).

Khi đó $\tan \alpha =\frac{\sin \alpha }{\cos \alpha }=\frac{-\frac{4}{5}}{-\frac{3}{5}}=\frac{4}{3}$ và $\cot \alpha =\frac{1}{\tan \alpha }=\frac{1}{\frac{4}{3}}=\frac{3}{4}$.

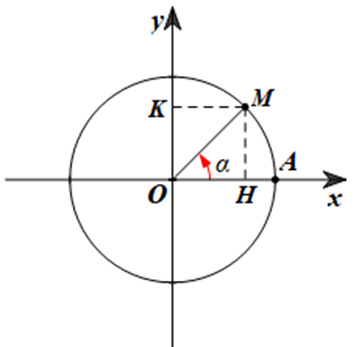
Hoạt động 10 trang 12 Toán 11 Tập 1: Tìm các giá trị lượng giác của góc lượng giác α = 45°.

Lời giải:

Lấy điểm M trên đường tròn lượng giác sao cho (OA, OM) = α = 45° (hình vẽ).

Gọi H, K lần lượt là hình chiếu của điểm M trên các trục Ox, Oy.

Khi đó, ta có: $\widehat{AOM}=\text{45}°$.

Theo hệ thức trong tam giác vuông HOM, ta có:

$x_M=OH=OM.cos\widehat{HOM}=1.c\text{os45}°=\frac{\sqrt{2}}{2}$;

$y_M=OK=MH=OM.\sin \widehat{HOM}=1.\sin \text{45}°=\frac{\sqrt{2}}{2}$.

Do đó $M\left(\frac{\sqrt{2}}{2};\frac{\sqrt{2}}{2}\right)$.

Vậy $\sin 45°=\frac{\sqrt{2}}{2};cos45°=\frac{\sqrt{2}}{2};$$\tan 45°=1;\cot 45°=1$.

Luyện tập 10 trang 12 Toán 11 Tập 1: Tính giá trị của biểu thức: $Q={\tan }^2\frac{\pi }{3}+{\sin }^2\frac{\pi }{4}+\cot \frac{\pi }{4}+cos\frac{\pi }{2}$.

Lời giải:

Ta có:$Q={\tan }^2\frac{\pi }{3}+{\sin }^2\frac{\pi }{4}+\cot \frac{\pi }{4}+cos\frac{\pi }{2}$

$={\left(\sqrt{3}\right)}^2+{\left(\frac{\sqrt{2}}{2}\right)}^2+1+0=3+\frac{1}{2}+1=\frac{9}{2}$.

Lời giải bài tập Toán 11 Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác Cánh diều hay khác:

• Giải Toán 11 trang 5

• Giải Toán 11 trang 6

• Giải Toán 11 trang 7

• Giải Toán 11 trang 8

• Giải Toán 11 trang 9

• Giải Toán 11 trang 10

• Giải Toán 11 trang 11

• Giải Toán 11 trang 14

• Giải Toán 11 trang 15