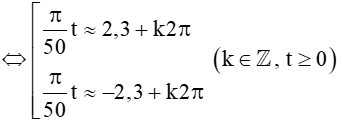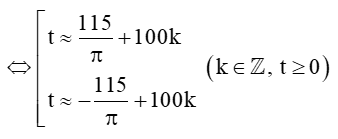Giải Toán 11 trang 32 Tập 1 Cánh diều

---

Với Giải Toán 11 trang 32 Tập 1 trong Bài 4: Phương trình lượng giác cơ bản Toán lớp 11 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 32.

Giải Toán 11 trang 32 Tập 1 Cánh diều

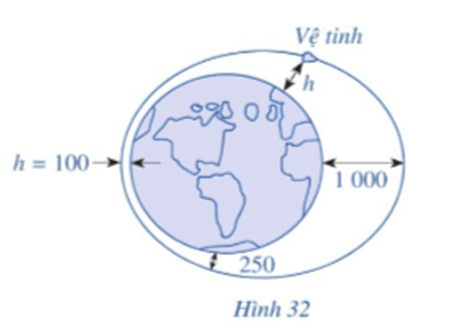
Câu hỏi khởi động trang 32 Toán 11 Tập 1: Một vệ tinh nhân tạo bay quanh Trái Đất theo một quỹ đạo là đường elip (Hình 32). Độ cao h (km) của vệ tinh so với bề mặt Trái Đất được xác định bởi công thức h = 550 + 450cos$\frac{\pi }{50}$t (Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2021), trong đó t là thời gian tính bằng phút kể từ lúc vệ tinh bay vào quỹ đạo. Tại thời điểm t bằng bao nhiêu thì vệ tinh cách mặt đất 1 000 km; 250 km; 100 km?

Trên thực tế, có nhiều bài toán dẫn đến việc giải một trong các phương trình có dạng: sinx = m, cosx = m, tanx = m, cotx = m, trong đó x là ẩn số, m là số thực cho trước. Các phương trình đó là các phương trình lượng giác cơ bản.

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

• Để vệ tinh cách mặt đất 1 000 km thì 550 + 450cos$\frac{\pi }{50}$t = 1 000

$\iff$450cos$\frac{\pi }{50}$t=450

$\iff$ cos$\frac{\pi }{50}$t = 1

$\iff$$\frac{\pi }{50}$t = k2$\pi$ (k$\in Z$, t$\ge$0)

$\iff$t = k2$\pi$.$\frac{50}{\pi }$ = 100k (k$\in Z${0; 1; 2; 3;...}

Vậy tại các thời điểm t = 100k (với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 1 000 km.

• Để vệ tinh cách mặt đất 250 km thì 550 + 450cos$\frac{\pi }{50}$t = 250

$\iff$ 450cos$\frac{\pi }{50}$t = -300

$\iff$ cos$\frac{\pi }{50}$t = -$\frac{2}{3}$

(Dùng máy tính cầm tay (chuyển về chế độ “radian”) bấm liên tiếp ta được kết quả gần đúng là 2,3)

Vậy tại các thời điểm t $\approx \pm \frac{115}{\pi }$+100k (với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 250 km.

• Để vệ tinh cách mặt đất 100 km thì 550 + 450cos$\frac{\pi }{50}$t = 100

$\iff$ 450cos$\frac{\pi }{50}$t = -450

$\iff$ cos$\frac{\pi }{50}$t = -1

$\iff$$\frac{\pi }{50}$t = $\pi$+k2$\pi$ (k$\in$Z, t$\ge$0).

$\iff$ t = 50+100k (k$\in${0;1;2;3;...}

Vậy tại các thời điểm t = 50 + 100k (với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 100 km.

Hoạt động 1 trang 32 Toán 11 Tập 1: Cho hai phương trình (với cùng ẩn x):

x² ‒ 3x + 2 = 0 (1)

(x – 1)(x – 2) = 0 (2)

a) Tìm tập nghiệm S₁ của phương trình (1) và tập nghiệm S₂ của phương trình (2).

b) Hai tập S₁, S₂ có bằng nhau hay không?

Lời giải:

a) Ta có:

x² ‒ 3x + 2 = 0 (1)

Suy ra x = 1 hoặc x = 2.

Vậy phương trình (1) có tập nghiệm S₁ = {1; 2}.

(x – 1)(x – 2) = 0 (2)

Suy ra x = 1 hoặc x = 2.

Vậy phương trình (2) có tập nghiệm S₂ = {1; 2}.

b) Hai tập S₁, S₂ bằng nhau vì cùng là tập {1; 2}.

Luyện tập 1 trang 32 Toán 11 Tập 1: Hai phương trình x – 1 = 0 và $\frac{x^2-1}{x+1}$=0 có tương đương không? Vì sao?

Lời giải:

Tập nghiệm của phương trình x – 1 = 0 là S₁ = {1}.

Tập nghiệm của phương trình $\frac{x^2-1}{x+1}$ là S₂ = {1}.

Vì S₁ = S₂ nên hai phương trình x – 1 = 0 và $\frac{x^2-1}{x+1}$=0 tương đương.

Lời giải bài tập Toán 11 Bài 4: Phương trình lượng giác cơ bản Cánh diều hay khác:

• Giải Toán 11 trang 33

• Giải Toán 11 trang 35

• Giải Toán 11 trang 37

• Giải Toán 11 trang 38

• Giải Toán 11 trang 40