Giải Toán 11 trang 33 Tập 1 Cánh diều
Với Giải Toán 11 trang 33 Tập 1 trong Bài 4: Phương trình lượng giác cơ bản Toán lớp 11 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 33.
Giải Toán 11 trang 33 Tập 1 Cánh diều
Hoạt động 2 trang 33 Toán 11 Tập 1: Khẳng định 3x ‒ 6 = 0 3x = 6 đúng hay sai?
Lời giải:
Phương trình 3x ‒ 6 = 0 có tập nghiệm S1 = {2}.
Phương trình 3x = 6 có tập nghiệm S2 = {2}.
Vì S1 = S2 nên hai phương trình 3x ‒ 6 = 0 và 3x = 6 tương đương
Khi đó ta viết 3x ‒ 6 = 0 3x = 6.
Vậy khẳng định 3x ‒ 6 = 0 3x = 6 là khẳng định đúng.
Luyện tập 2 trang 33 Toán 11 Tập 1: Giải phương trình: (x – 1)2 = 5x – 11.
Lời giải:
Ta có: (x – 1)2 = 5x – 11.
x2 – 2x + 1 – (5x – 11) = 0
x2 – 2x + 1 – 5x + 11 = 0
x2 – 7x + 12 = 0
x = 3 hoặc x = 4.
Vậy tập nghiệm của phương trình đã cho là S = {3; 4}.
Hoạt động 3 trang 33 Toán 11 Tập 1:
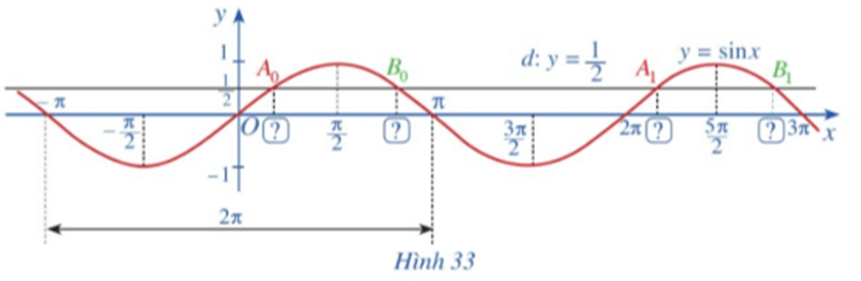
a) Đường thẳng d: y = cắt đồ thị hàm số y = sinx, x ∈ [‒π; π] tại hai giao điểm A0, B0 (Hình 33). Tìm hoành độ của hai giao điểm A0, B0.
b) Đường thẳng d: y = cắt đồ thị hàm số y = sinx, x ∈ [π; 3π] tại hai giao điểm A1, B1 (Hình 33). Tìm hoành độ của hai giao điểm A1, B1.
Lời giải:
a) Với x ∈ [‒π; π] ta thấy sin x = tại x = và x = .
Do đó đường thẳng d: y = cắt đồ thị hàm số y = sinx, x ∈ [‒π; π] tại hai giao điểm A0, B0 có hoành độ lần lượt là và .
b) Với x ∈ [π; 3π] ta thấy sin x = tại x = và x = .
Do đó đường thẳng d: y = cắt đồ thị hàm số y = sinx, x ∈ [π; 3π] tại hai giao điểm A1, B1 có hoành độ lần lượt là và .
Lời giải bài tập Toán 11 Bài 4: Phương trình lượng giác cơ bản Cánh diều hay khác: