Giải Toán 11 trang 38 Tập 1 Cánh diều

---

Với Giải Toán 11 trang 38 Tập 1 trong Bài 4: Phương trình lượng giác cơ bản Toán lớp 11 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 38.

Giải Toán 11 trang 38 Tập 1 Cánh diều

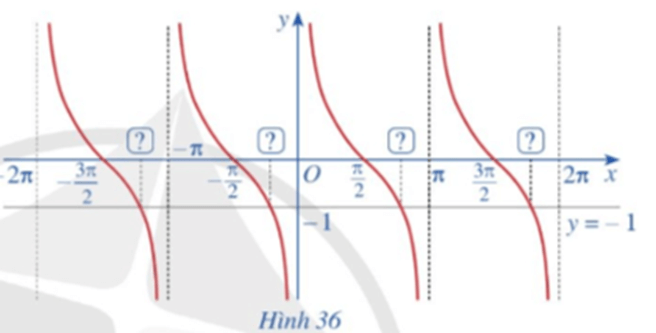
Hoạt động 6 trang 38 Toán 11 Tập 1: Quan sát các giao điểm của đồ thị hàm số y = cotx và đường thẳng y = ‒1 (Hình 36).

a) Từ hoành độ giao điểm của đồ thị hàm số y = cotx và đường thẳng y = ‒1 trên khoảng (0; π), hãy xác định tất cả các hoành độ giao điểm của hai đồ thị đó.

b) Có nhận xét gì về nghiệm của phương trình cotx = ‒1?

Lời giải:

a) Với x ∈ (0; π), ta thấy cotx = ‒1 tại x=$\frac{3\pi }{4}$.

Do đó đường thẳng y = ‒1 cắt đồ thị hàm số y = cotx trên khoảng (0; π) tại điểm có hoành độ là $\frac{3\pi }{4}$.

Do hàm số y = cotx tuần hoàn với chu kì là π nên đường thẳng y = ‒1 cắt đồ thị hàm số y = cotx tại các điểm có hoành độ là x=$\frac{3\pi }{4}$+k$\pi$ (k$\in$Z).

b) Phương trình cotx = ‒1 có các nghiệm là x=-$\frac{3\pi }{4}$+k$\pi$.

Luyện tập 8 trang 39 Toán 11 Tập 1:

a) Giải phương trình: cotx = 1.

b) Tìm góc lượng giác x sao cho cotx = cot(‒83°).

Lời giải:

a) Do cotx = 1 nên cotx = cot$\frac{\pi }{4}$$\iff$ x=$\frac{\pi }{4}$+k$\pi$ (k$\in$Z).

Vậy phương trình cotx = 1 có các nghiệm là x=$\frac{\pi }{4}$+k$\pi$ với k ∈ ℤ.

b) cotx = cot(‒83°)

$\iff$ x = ‒83° + k180° (k ∈ ℤ).

Vậy các góc lượng giác x cần tìm là x = ‒83° + k180° với k ∈ ℤ.

Lời giải bài tập Toán 11 Bài 4: Phương trình lượng giác cơ bản Cánh diều hay khác:

• Giải Toán 11 trang 32

• Giải Toán 11 trang 33

• Giải Toán 11 trang 35

• Giải Toán 11 trang 37

• Giải Toán 11 trang 40