Bài 7 trang 82 Toán 11 Tập 2 Chân trời sáng tạo

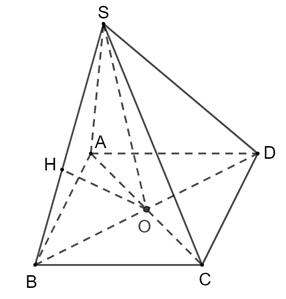
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a và có O là giao điểm hai đường chéo của đáy.

Giải Toán 11 Bài 4: Khoảng cách trong không gian - Chân trời sáng tạo

Bài 7 trang 82 Toán 11 Tập 2: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a và có O là giao điểm hai đường chéo của đáy.

a) Tính khoảng cách giữa hai đường thẳng AC và SB.

b) Tính thể tích của khối chóp.

Lời giải:

Bài 7 trang 82 Toán 11 Tập 2 Chân trời sáng tạo

a) Kẻ OH ⊥ SB (H $\in$ SB)

S.ABCD là hình chóp tứ giác đều $\Rightarrow$ SO ⊥ (ABCD) $\Rightarrow$ SO ⊥AC.

Tứ giác ABCD là hình vuông suy ra AC ⊥ BD $\Rightarrow$ AC ⊥(SBD) $\Rightarrow$ AC ⊥ OH.

Mà $OH ⊥ SB$

Do đó d(AC, SB) = OH

• Xét ΔABD vuông tại A, ta có:

$BD = \sqrt{{AB}^{2} + {AD}^{2}} = a \sqrt{2} \Rightarrow BO = \frac{1}{2} BD = \frac{a \sqrt{2}}{2}$

• Xét ΔSBO vuông tại O, ta có:

$SO = \sqrt{{SB}^{2} - {BO}^{2}} = \frac{a \sqrt{2}}{2}$

• Xét ΔSBO vuông tại O có SO = BO nên ΔSBO vuông cân tại O

Suy ra OH vừa là đường cao, vừa là đường trung tuyến.

Do đó $OH = \frac{1}{2} SB = \frac{a}{2}$

Vậy $d (AC, SB) = \frac{a}{2}$

b) $S_{ABCD} = a^{2}$ .

Thể tích khối chóp là: $V = \frac{1}{3} . SO . S_{ABC D} = \frac{a^{3} \sqrt{2}}{6} .$

Lời giải bài tập Toán 11 Bài 4: Khoảng cách trong không gian hay, chi tiết khác: