Giải Toán 11 trang 68 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 68 Tập 1 trong Bài 1: Giới hạn của dãy số Toán lớp 11 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 68.

Giải Toán 11 trang 68 Tập 1 Chân trời sáng tạo

Thực hành 4 trang 68 Toán 11 Tập 1: Tính tổng của cấp số nhân lùi vô hạn: $1+\frac{1}{3}+{\left(\frac{1}{3}\right)}^2+\mathrm{...}+{\left(\frac{1}{3}\right)}^n+\mathrm{...}$

Lời giải:

Tổng của cấp số nhân lùi vô hạn có số hạng đầu u₁ = 1 và công bội là $q=\frac{1}{3}<1$ là:

$S_n=1+\frac{1}{3}+{\left(\frac{1}{3}\right)}^2+\mathrm{...}+{\left(\frac{1}{3}\right)}^n+\mathrm{...}=\frac{1}{1-\frac{1}{3}}=\frac{3}{2}$.

Vận dụng 1 trang 68 Toán 11 Tập 1: Từ tờ giấy, cắt một hình tròn bán kính R (cm) như Hình 3a. Tiếp theo, cắt hai hình tròn bán kính $\frac{R}{2}$ rồi chồng lên hình tròn đầu tiên như Hình 3b. Tiếp theo, cắt bốn hình tròn bán kính $\frac{R}{4}$ rồi chồng lên các hình trước như Hình 3c. Cứ thế tiếp tục mãi. Tính tổng diện tích của các hình tròn.

Lời giải:

Nội dung đang được cập nhật...

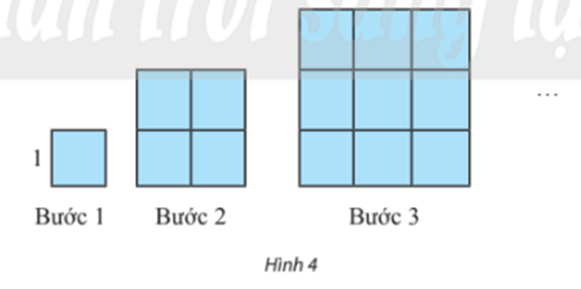
Hoạt động khám phá 5 trang 68 Toán 11 Tập 1: Dựng một dãy hình vuông bằng cách ghép từ các hình vuông đơn vị (cạnh bằng 1 đơn vị độ dài) theo các bước như Hình 4. Kí hiệu u_n (đơn vị diện tích) là diện tích hình vuông dựng được ở bước thứ n.

a) Với n như thế nào thì u_n vượt quá 10 000; 1 000 000?

b) Cho hình có diện tích S. Với n như thế nào thì u_n vượt quá S?

Lời giải:

a) Diện tích của hình vuông u_n dựng ở bước thứ n là: u_n = n² (đơn vị diện tích).

Để u_n vượt quá 10 000 thì n² > 10 000 ⇔ n > 100.

Để u_n vượt quá 1 000 000 thì n² > 1 000 000 ⇔ n > 1000.

b) Để u_n vượt quá S thì u_n > S ⇔ n² > S ⇔ n > $\sqrt{S}$.

Lời giải bài tập Toán 11 Bài 1: Giới hạn của dãy số Chân trời sáng tạo hay khác:

• Giải Toán 11 trang 64

• Giải Toán 11 trang 65

• Giải Toán 11 trang 66

• Giải Toán 11 trang 69

• Giải Toán 11 trang 70